"Humans, it seems, know things; and what they know helps them do things." -Actual Quote from your Textbook

That line has always amused me, but belies some important points about the first type of intelligence that we'll see in this course: logic and reasoning.

What are some of the main traits of human intelligence that likely facilitate our ability to act as rational agents?

Inference is the ability to take knowledge about the mechanics of an environment (rules), marry those to observations about the environment (facts), and then deduce new facts as a result (inferences).

Humans perform inference with relative ease -- if you're reading along, you likely foresaw the conclusion of the above example before you read it.

At what tier of the Pearlian Causal Hierarchy would you find the capacity for logical inference?

At \(\mathcal{L}_2\) or above! This is certainly not associational.

Why is the capacity for inference a desirable trait for our artificial agents?

Plainly the capacity for inference is a large step towards generalized intelligence, and will be one of our first goals towards designing logical agents.

Looking at the human traits leading to inference, what challenges do you envision for this task; what will we have to formalize?

We'll begin by considering a motivating example, and then cover the classical representation of knowledge and inference reaching all the way back to the days of Socrates...

Thus far (CMSI 282/2130 and before) we have been examining perfect information, offline search problems wherein our agent plans its moves before acting from some problem specification.

Of course, in more realistic examples, our agent may not possess all relevant decision-making information about the environment at the get-go, and must instead discover key pieces as it acts.

Offline agents are those that may plan with all relevant information before acting; online agents are those that must acquire relevant pieces of the plan as they act, generally involving some exploration.

We can start to see where we will need the aid of inference in the following, motivating example:

Watching Our Steps

---

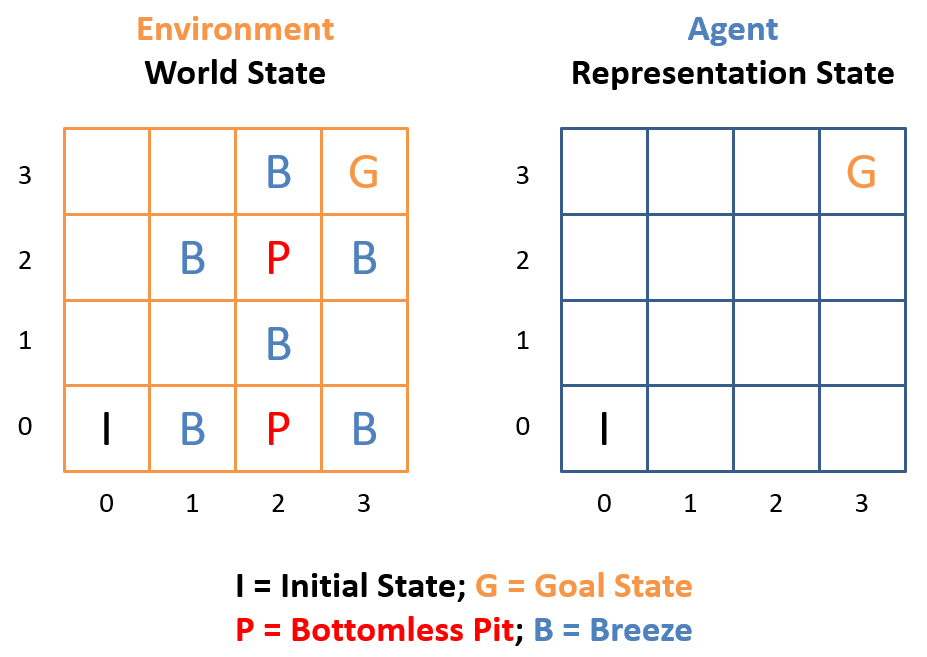
Consider the following variant to the classic Maze Pathfinder (a variant of your textbook's strange and needlessly complicated "Wumpus World" [the hell is a Wumpus?]):

• The bad news:

  • Mazes can now feature dangerous bottomless pits \(P\) of doom! If our agent falls into a pit, they will fall for all of eternity, which is generally something we'd like to avoid.

  • The locations of pits are not known to the agent a priori, and so they must instead deduce the locations of pits as best as possible.

• The good news:

  • Each Pit (being bottomless and all) generates a current of wind in the cells adjacent to it, which we'll label as Breezes, \(B\). Agents will be able to use sensors to detect this breeze.

  • The Initial and Goal states are known and will not contain Pits.

  • A cautious and logical agent will thus need to scout to find safe passage to the Goal state.

Since this is an imperfect information problem, we must be careful to make a distinction:

An agent's representation of the environment is their choice of how to model its key features; this representation, although attempting to be accurate, may differ from the world in reality.

The following is an example of our new PitfallMazes with an agent's starting representation.

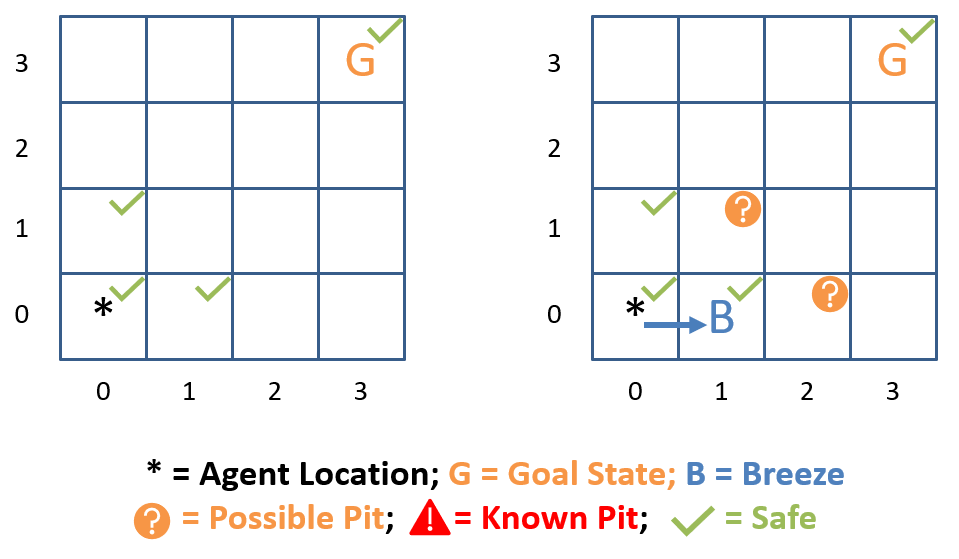
Will a classical search approach like A* alone solves these problems?

No! We need to involve extra information about the logical confines of the problem in order to safely navigate around the pits.

Since the agent should act cautiously to reach the goal, it will need to logically deduce a safe path using its percepts.

What kinds of facts would our agent need to track in order to logically navigate these mazes?

(1) Where breezes are felt, (2) how that translates to inferences about pit locations, and (3) which tiles are deduced to be safe.

Trace the logical steps the agent would need to take in order to find the proper route to the goal.

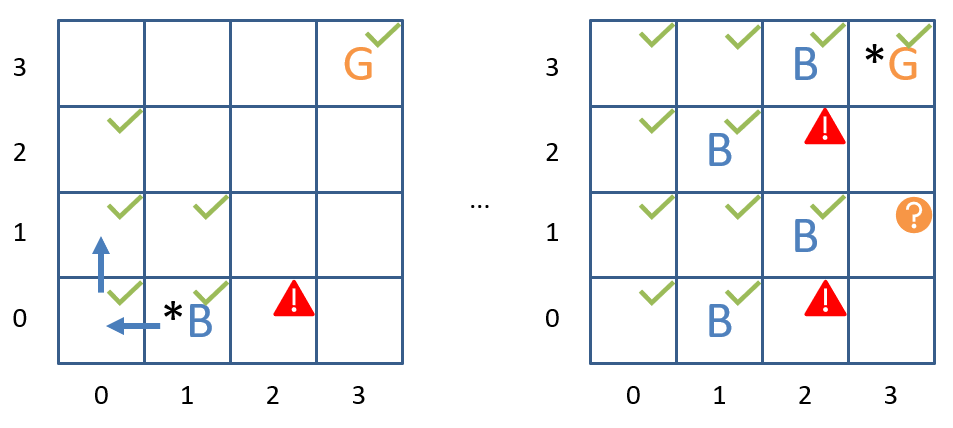
Plainly, formalizing the logic that feeds into these deductive agents needs some strong foundations, which we'll examine next!

The first steps towards creating logical agents began with roots in philosophical discourse.

In philosophy and logic, what is the traditional data type of discourse?

Good old Boolean values that determine if something is either true or false (see the Socrates example at the start).

Let's start by reasoning over systems of simple, Boolean expressions that determine small aspects of truth in the environment, and then see how they can combine to perform inference.

This will lead to us designing who can make deductions about their environments.

A knowledge-based agent is an intelligent system whose known information is stored in a knowledge-base (KB) that consists of logical sentences that represent assertions about the world.

As it turns out, some representation languages (like the one we will preview) will not distinguish between these two classes, but will still help us think about our agents' knowledge.

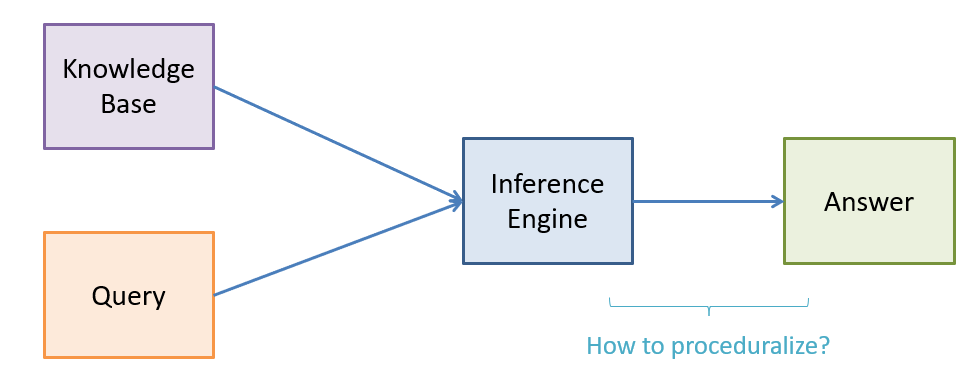
The process of inference is handled by an inference engine, which is parameterized by (1) a knowledge-base and (2) a query and produces an answer to that query.

Pictorially, this process looks like:

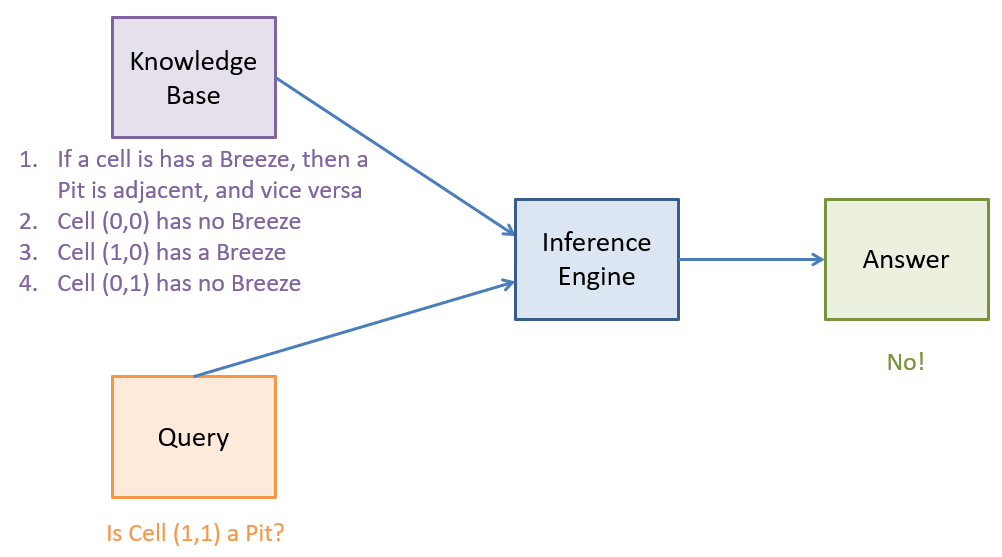
Which are the rules and which are the facts in the KB above?

Rules: (1); Facts: (2-4)

In this section, we will look at the most basic, but still powerful, knowledge representation language that is related to Boolean logic.

Propositional Logic is a knowledge representation language in which propositions (T/F variables) make assertions about aspects of the reasoning environment.

Let's look at how it works!

Propositional Syntax

---

The syntax of propositional logic defines what constitutes a logical expression.

Propositional symbols are "placeholders" (think: variables) for truth values, and include two "constant" symbols: \(True\) or \(T\) to denote the "always true" proposition, and \(False\) or \(F\) to denote the "always false."

Atomic sentences are propositional sentences containing only a single propositional symbol.

If we use \(B_{x,y}\) to indicate the proposition that a Breeze is in the given \((x,y)\) coordinate, then an atomic sentence would contain only something like \(B_{1,0}\) to indicate the Breeze "status" of tile \((1,0)\).

Note that depending upon the particular maze, \(B_{1,0}\) may be True or False (discussed more in semantics, to follow).

Of course, it would be fairly weak if we could only express propositions about atomic elements of the environment.

The power of inference comes from our ability to reason over relationships between propositions.

Complex sentences are constructed from simpler sentences using logical grouping \(()\) and connectives.

Now that we know the basic syntax of propositional logic, let's consider some examples translating English sentences into Propositional ones.

Translate each of the following English sentences into propositional ones, letting \(B_{x,y}\) indicate that a Breeze is in cell \((x,y)\) and letting \(P_{x,y}\) indicate that a Pit is in cell \((x,y)\).

  #1 "There is no Pit at (0,0)"
  
  #2 "There is no Pit at (0,0) nor is there a Pit at (3,3)"
  
  #3 "There is a Breeze in (1,0), if and only if there is a
  pit in an adjacent (legal) cell"

Propositional Semantics

---

Now that we have a gist for the format of legal propositional sentences, let's consider what, precisely, these logical sentences mean.

A world \(w\) is a possible instantiation of all propositions (i.e., an assignment of \(True, False\) to all props.)

For example, in some worlds (hypothetical or reality), there is a Pit at \((1, 1)\) in which case \(P_{1,1} = True\), but in others there may not be.

Worlds are to states of the environment as propositional sentences are to assertions about the state of the world.

Propositional semantics define the rules that decide whether a given sentence is \(True\) or \(False\) in some world.

So what are these rules? These semantics?

It turns out the rules can be defined recursively, since all complex sentences are defined atop combinations of atomic ones.

Semantics for Atomic Sentences

---

• \(True\) is true in every world and \(False\) is false.

• Every proposition (e.g., \(P_{1,1}\)) is assigned a truth value in the world.

For example, one world for three propositions \(A, B, C\) might look like: \(\{A = True, B = False, C = True \}\)

The above should come as no surprise, but now let's look at how to put everything together.

Semantics for Complex Sentences

---

We'll assign truth interpretations to each of our 5 connectives (below, \(P, Q\) are propositions):

• \(\lnot P\) is true only in worlds where \(P = False\)

• \(P \land Q\) is true only in worlds where \(P = True\) and \(Q = True\)

• \(P \lor Q\) is true only in worlds where either \(P = True\) or \(Q = True\) or both are \(True\).

• \(P \Rightarrow Q\) is true unless \(P = True\) and \(Q = False\) (interpretted: "If \(P\) is true, then \(Q\) is true, otherwise, the condition isn't satisfied, so the consequence needn't follow.")

  Implication is often the most confusing when the condition P is not satisfied. Think of it this way: If I say "If it's raining out, then the sidewalk will be wet," that rule may still be true even if it is not raining out and the sidewalk is wet.

• \(P \Leftrightarrow Q\) is true if and only if \(P = Q\)

Truth Tables

---

The semantic rules defined above allow us to assign a truth value to every sentence given a particular world.

Suppose we have 2 propositions, \(P, Q\) -- how many possible worlds are there? How many for \(n\) propositions?

For just \(P, Q\), 4 possible worlds. In general: \(2^n\) possible worlds.

So, another way to consider the semantics for each sentence (atomic or complex) is to provide a corresponding mapping from the sentence to a truth value.

Truth tables map a sentence and each possible world to a truth value.

Consider the truth table associated with 2 propositions \(P, Q\).

World	P	Q	\(\lnot P\)	\(P \land Q\)	\(P \lor Q\)	\(P \Rightarrow Q\)	\(P \Leftrightarrow Q\)
\(w_1\)	F	F	T	F	F	T	T
\(w_2\)	F	T	T	F	T	T	F
\(w_3\)	T	F	F	F	T	F	F
\(w_4\)	T	T	F	T	T	T	T

Two sentences are logically equivalent if they have the same truth-table values for each world.

Note a couple of remarks on our implication and biconditional connectives:

• \(P \Rightarrow Q\) is logically equivalent to \(\lnot P \lor Q\)

• \(P \Leftrightarrow Q\) is logically equivalent to \((P \Rightarrow Q) \land (Q \Rightarrow P)\)

We'll make use of these equivalences in the next lecture...

Equipped with this syntax and semantics, we'll see how inference works and derive a (pretty computationally tough!) algorithm to proceduralize it!

Is Socrates actually mortal? Story at 11!

With the syntax and semantics of propositional logic in hand, we got a glimpse of how these tools can start to form the logical "picture" our agents have of their environments.

Recall our motivating problem, which involved our Maze Pathfinder but with the added trouble of needing to navigate bottomless pits in the environment.

Notably, in this setting, our knowledge base can grow over time from its initial state through what is known as online learning, where the agent acquires experiences from the environment in which it's deployed.

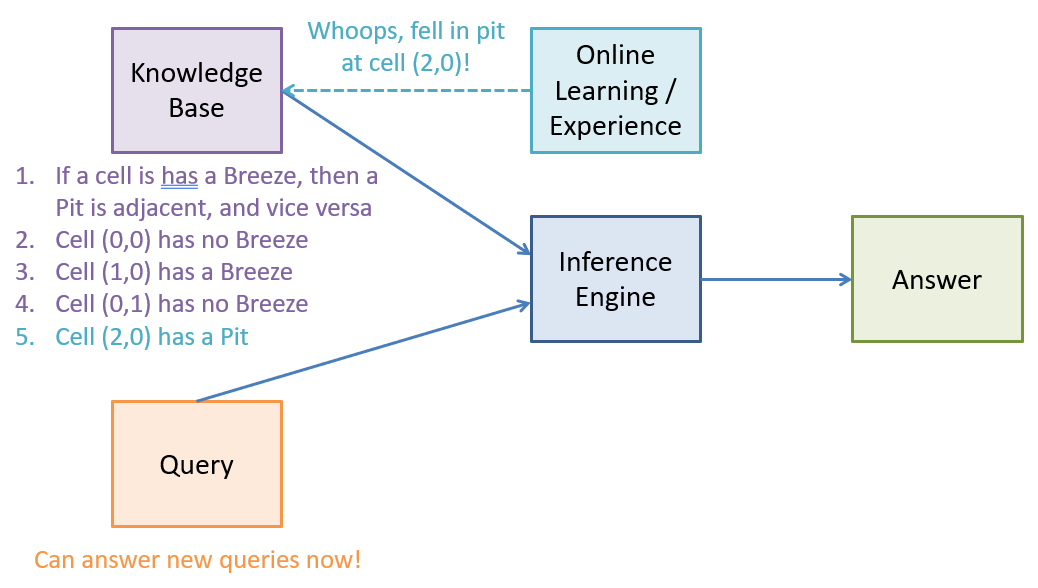
So, let's begin by considering: what should be contained in our agent's knowledge base at the onset of its exploration?

What propositions (i.e., symbols / variables for T/F aspects of the environment) will we need in order to avoid Pits?

\(P_{x,y}\) to indicate that a Pit exists in tile \((x,y)\) and \(B_{x,y}\) to indicate a Breeze exists in tile \((x,y)\). In implementation, we really only need to know where there are and aren't pits if that's all we care about, but a more general implementation might care about where breezes exist, so we'll use both here.

What rules (i.e., propositional sentences that describe how the world works) should we include for our problem? How to phrase them?

We must indicate that if a Breeze exists at some tile, then there must be at least 1 Pit in neighboring tiles; formally: $$B_{x,y} \Leftrightarrow P_{x-1,y} \lor P_{x+1,y} \lor P_{x,y-1} \lor P_{x,y+1} ~ \forall ~ x,y$$

Note: propositional logic demands that these rules exist for every tile in the maze!

This might seem wasteful (it is) but is a consequence of propositional logic not being a form a higher order reasoning, wherein we could reason over patterns of logical sentences.

This approach (which does exist) is called first order logic, and is unfortunately out of scope for this class, but is not much different than the algorithms we'll review herein.

Now that we have our rule(s) formalized, we just need to include all of our current observations about the environment.

What facts (i.e., typically atomic sentences that are true in the currently observed environment) should we include for the initial state of our problem?

(1) We know that pits do not exist at either the initial nor goal state: \(\lnot P_{0,0} \land \lnot P_{3,3}\). (2) We know that there is no Breeze in the initial state \(\lnot B_{0,0}\)

Since we are claiming that all of these rules and facts are asserted true in our environment, how can we view our KB in terms of propositional connectives?

Our KB is simply a giant complex sentence in which all rules and facts are conjoined, with the format: $$KB = Rule_1 \land Rule_2 \land ... \land Fact_1 \land Fact_2 \land ...$$

What happens if our agent discovers a new fact during exploration of the Maze?

We simply add that to the existing rules and facts in the KB!

Acquiring facts through exploration adds knowledge to the KB through conjunction, defining a "tell" operation: $$KB.tell(new\_fact): KB = KB \land new\_fact$$

For convenience (for both humans and in programmatic application) KB's in the format of conjoined rules and facts often enumerate the conjoined sentences, for example, the knowledge-base in our Pitfall Maze might look like:

$$KB = (B_{1,0} \Leftrightarrow P_{0,0} \lor P_{1,1} \lor P_{2,0}) \land ... \land \lnot P_{0,0} \land \lnot P_{3,3} \land \lnot B_{0,0} \land ...$$

Is oft represented as:

1. \(B_{1,0} \Leftrightarrow P_{0,0} \lor P_{1,1} \lor P_{2,0}\)

2. \(...\)

3. \(\lnot P_{0,0}\)

4. \(\lnot P_{3,3}\)

5. \(\lnot B_{0,0}\)

6. \(...\)

Of course, now that we have a basic understanding of how the KB looks, we need to formalize some mechanisms that will be important for inference.

Recall our picture of the inference engine that we are hoping to design.

Now that we have a picture of what our KB looks like (section above), let's consider a couple of different ways of answering some inference queries, starting with the brute force approach.

Propositional Inference is the process of determining the truth of certain sentences that are not stated explicitly in a KB.

In other words, inference allows us to make claims by way of propositional sentences that can be inferred from our KB, though may not be given.

In other, other words, we take what we know, and use that knowledge to deduce something that we knew, but wasn't obvious.

So, we'll consider the simplest interpretation of inference first:

We've seen the vocabulary "model" apply to an instantiation of truth values to propositions in the KB: \(\{P_1 = True, P_2 = False, ...\}\)

For propositional sentence \(\alpha\), we say that its models are the set of all worlds \(\{w_1, w_2, ...\}\) in which \(\alpha\) is true, notated: $$M(\alpha) = \{m_1, m_2, ...\}$$

Consider a simple system with two propositions, \(R, P\), and and a sentence \(\alpha = \lnot R\).

World	\(R\)	\(P\)	\(\alpha = \lnot R\)
\(w_0\)	F	F	T
\(w_1\)	F	T	T
\(w_2\)	T	F	F
\(w_3\)	T	T	F

Trivially, in the above, we can see that the models of our sentence are any world in which it is true, so: \(M(\alpha) = \{w_0, w_1\} \).

This means that if some knowledge base, KB, contained the sentence \(\alpha\), and it is (hopefully) faithful to reality, then worlds \(\{w_2, w_3\}\) are not possible!

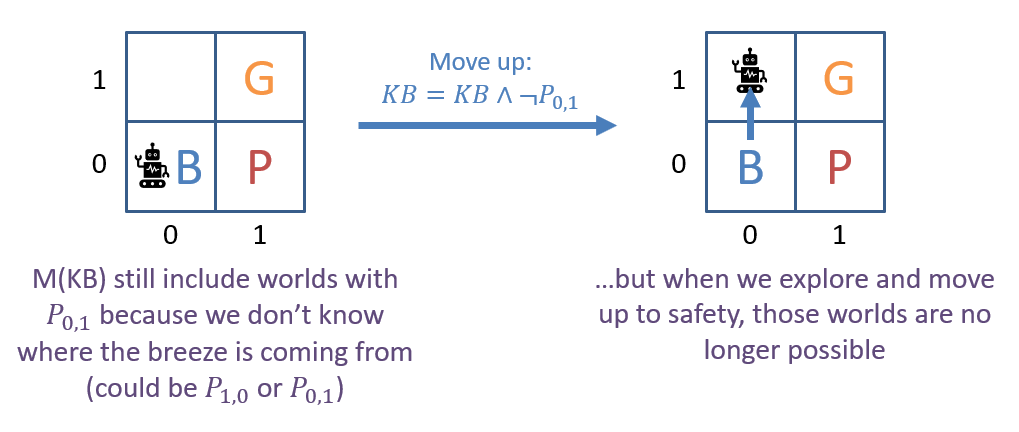
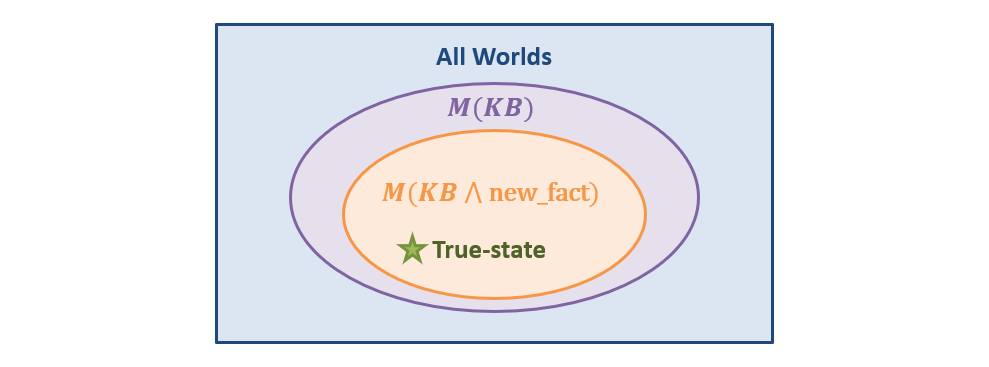
The tell operation of a KB is special in terms of the KB's models (the worlds that are consistent with it) because every time a new fact is acquired, the models of the KB shrink (which is a good thing, because that means we're getting closer to knowing the *one real* state of the world). Viz.: $$M(KB \land new\_fact) \subseteq M(KB)$$

Visually, this looks like:

Note: this means that our KB excludes certain worlds / models from consideration -- rightly so, since some are not fidelitous representations of reality.

So now, we return to our inference engine:

Given some query, we want to know if the query follows from the knowledge encoded in the KB or not.

Consider that we wish to query our KB to determine if a Pit exists at (2,0), i.e., we want to know the truth value of \(P_{2,0}\) in \(M(KB)\).

In terms of \(M(KB)\), there are 3 possible answers to this query. What are they, and how can we phrase them in terms of \(M(KB)\)?

As it turns out, we can characterize the above using a criteria known as entailment:

For two propositional sentences \(\alpha, \beta\) we say that \(\alpha\) entails \(\beta\) (meaning \(\beta\) follows from \(\alpha\)), written \(\alpha \vDash \beta\) if the models of \(\alpha\) are a subset of the models of \(\beta\), or formally: $$\alpha \vDash \beta \Leftrightarrow M(\alpha) \subseteq M(\beta)$$

Entailment is the same idea as implication, except that implication is typically used as an asserted rule in the *symbolic* KB and entailment is proved by examining *models.*

Pictorially, entailment looks like:

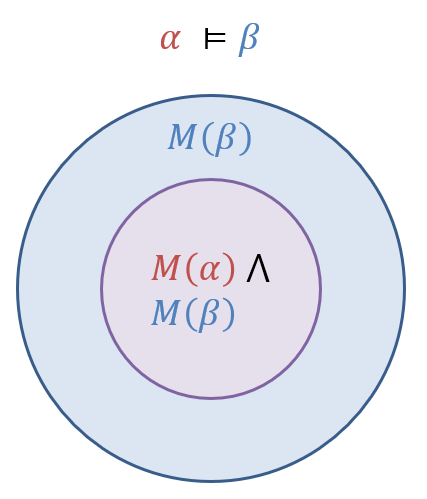
So, returning to our example of determining the pit status at \(\alpha = P_{2,0}\), what our KB tells us about the three cases can be depicted as follows:

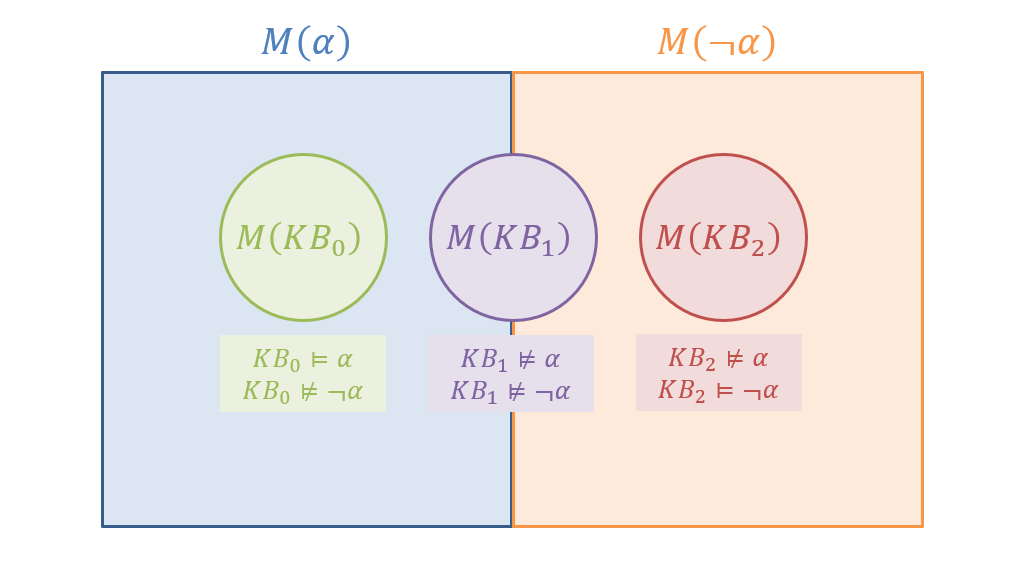
Punchline: in order to determine the state of entailment for some sentence \(\alpha\) in our KB, you'll need *at most* 2 tests to determine if you have enough information to make a conclusion: testing if (1) \(M(KB) \vDash \alpha\) and (2) \(M(KB) \vDash \lnot \alpha\), the answers of which will match one of the above image's 3 cases.

As an illustrative example, consider a system with 3 propositions, \(R, P, S\) and a KB consisting of the sentence \(KB = (\lnot P \lor S) \land \lnot R\). We can similarly diagram the models of two additional sentences, \(\lnot R\) and \(\lnot P\).

World	\(R\)	\(P\)	\(S\)	\(KB = (\lnot P \lor S) \land \lnot R\)	\(\lnot R\)	\(\lnot P\)
\(w_0\)	F	F	F	T	T	T
\(w_1\)	F	F	T	T	T	T
\(w_2\)	F	T	F	F	T	F
\(w_3\)	F	T	T	T	T	F
\(w_4\)	T	F	F	F	F	T
\(w_5\)	T	F	T	F	F	T
\(w_6\)	T	T	F	F	F	F
\(w_7\)	T	T	T	F	F	F

Now, detailing the models of each sentence:

Sentences	Models (set of worlds, enumerated)
\(R\)	\(\{4, 5, 6, 7\}\)
\(\lnot R\)	\(\{0, 1, 2, 3\}\)
\(P\)	\(\{2, 3, 6, 7\}\)
\(\lnot P\)	\(\{0, 1, 4, 5\}\)
\(KB = (\lnot P \lor S) \land \lnot R\)	\(\{0, 1, 3\}\)

Using the above, we can reflect:

Does \(KB \vDash R\)?

No, since \(M(KB) = \{0, 1, 3\}\) are not a subset of \(M(R) = \{4, 5, 6, 7\}\). However, we would not immediately conclude that \(KB \vDash \lnot R\) until verifying that \(M(KB) = \{0, 1, 3\} \subseteq M(\lnot R) = \{0, 1, 2, 3\}\), which is indeed the case, and so we conclude \(KB \vDash \lnot R\)

Does \(KB \vDash P\)?

No, since \(M(KB) = \{0, 1, 3\}\) are not a subset of \(M(P) = \{2, 3, 6, 7\}\). However, we would not immediately conclude that \(KB \vDash \lnot P\), since \(M(KB) = \{0, 1, 3\} \not \subseteq M(\lnot P) = \{0, 1, 4, 5\}\), so we know that the \(KB\) does not have enough information to make assertions about proposition \(P\).

So... now, back to our Maze Pitfall problem...

Using the notion of entailment, how could we determine if our KB can answer whether or not a Pit exists in (0,2)?

Find out if \(KB \vDash P_{2,0} \Leftrightarrow M(KB) \subseteq M(P_{2,0}) \) or \(KB \vDash \lnot P_{2,0} \Leftrightarrow M(KB) \subseteq M(\lnot P_{2,0}) \). If one of those queries returns true, we know that we've reached a definitive answer. If both queries return false, we know that our KB cannot make a determination with the facts available.

In other words, if we show that, for every model in which our KB is true, our query is true as well, then the KB entails that query (i.e., the query follows).

This brute force procedure is known as model enumeration, since to check models of the KB and the query, we would need to consider their truth value in all possible models.

What's the problem with this brute force approach?

That's a lot of models to check! Note that for \(n\) propositions, we would have to check \(2^n\) models to construct the sets \(M(KB)\) and \(M(P_{2,0})\)!

Plainly then, this method does not scale for large systems... so, perhaps instead, we can get clever with the symbolic representation of propositions in our KB and find a more efficient way to answer our query...