Inference: Theorem Proving

Since we can't proceduralize model enumeration for settings with large numbers of propositions, let's consider whether we can perform inference from a strictly symbolic standpoint (i.e., using the KB and contained sentences alone).

Propositional Theorem Proving is the process of showing a KB entails a sentence without needing to consult the individual models of the system.

In other words, theorem proving allows us to perform inference at the symbolic level, rather than needing to evaluate the symbols for their truth values in every world.

Let's start by considering some aspects of our KB that have an intuitive lean toward inference: implications.

Consider two propositions: $R$ = whether or not it is raining out, $W$ = whether or not the sidewalk is wet.

Suppose in this setting we have the following KB:

KB:

"If it is raining, then the sidewalk will be wet"

1. $R \Rightarrow S$

"It is raining"

2. $R$

If we wish to query our KB as to whether or not the sidewalk is wet, how does the KB above provide an answer?

Since we wish to show that $KB \vDash S \Leftrightarrow M(KB) \subseteq M(S)$, it is sufficient to conclude that, since we have the rule "if R, then S" and the fact "R", we should be able to derive an inferred fact "S". Adding "S" to our KB (a conjunction of sentences) thus shows that $KB \vDash S$.

Indeed, the ability to take a rule and say "we've satisfied the premise for this rule, therefore we may infer the conclusion" has a known formula in philosophical discourse:

Modus Ponens (literally, "mood that affirms") is a rule of logic asserting that when an implication's premise (i.e., $P$ in $P \Rightarrow Q$) is met, then the conclusion (i.e., $Q$ in $P \Rightarrow Q$) may be inferred (i.e., added as an inferred fact to the KB). Formally: $$\frac{(\alpha \Rightarrow \beta) \land \alpha}{\beta}$$

If our $KB = ... \land \alpha \land ... $ it is a simple exercise to show that $KB \vDash \alpha$ as well.

This has a nice intuitive binding: if we've satisfied the premise of an implication as true, then its conclusion must be true as well, and so we can add its conclusion to our KB.

If the inferred sentence is our query, then we know the KB must have entailed it to begin with -- we just needed to expose it explicitly.

If our inference engine only knew about the Modus Ponens inference rule, how do we proceduralize inference? What would the stopping conditions look like?

(1) Repeatedly find rule premises that are satisfied, (2) add satisfied rules' conclusions to KB, (3) stop whenever KB contains query or when no more rules can be satisfied.

Plainly this is an exhaustive approach that might meander to the solution without any sort of guiding heuristic -- we can even consider it a type of search wherein the actions are applications of Modus Ponens, and the goal is to find the query sentence.

However, this approach suffers some issues in the case of general inference...

If our inference engine only knew about the Modus Ponens inference rule, would there be any inferences that it might miss? Consider the following example, and determine an inference that it *should* be able to deduce.

KB:

"If it is raining, then the sidewalk will be wet"

1. $R \Rightarrow S$

"The sidewalk is dry"

2. $\lnot S$

We *should* be able to figure out that it must not be raining out ($\lnot R$) given that the sidewalk is dry, but because our rule is in an implication in the other direction, we wouldn't be able to deduce this *using only modus ponens and the format of our KB.*

This gives us a TODO list:

Find a more general KB format that won't miss out on the directionality of if-then rules
Find a more general inference procedure compared to modus ponens that will be able to exploit this format

We'll examine this format next and then see how to apply the more general approach.

Knowledge Base Properties

Since we know that a KB is just a large, logical sentence (at some level of abstraction), an alternative title for this section would be "sentence properties."

There are certain qualities of how logical sentences are structured that can give us some powerful algorithmic benefits, and address some of the shortcomings from an inference engine equipped only with Modus Ponens.

We'll start by motivating these properties:

In an earlier lecture, we noticed that an implication $P \Rightarrow Q$ is logically equivalent to another sentence involving $P, Q$; what is the logical equivalence?

$(P \Rightarrow Q) \equiv (\lnot P \lor Q)$. (Note: $\equiv$ and $\Leftrightarrow$ mean the same thing, but using $\equiv$ makes it clear that these are logically equivalent and not a new compound sentence containing a biconditional).

Why is this signficant?

Consider a KB containing: (1) $P \Rightarrow Q$ and (2) $\lnot Q$. What inference should we be able to make? Show the steps of your proof.

$$\begin{eqnarray} P \Rightarrow Q &\equiv& \lnot P \lor Q \\ &\equiv& Q \lor \lnot P \\ &\equiv& \lnot Q \Rightarrow \lnot P \end{eqnarray}$$ Thus, by Modus Ponens, $ (\lnot Q \Rightarrow \lnot P) \land \lnot Q $, we should infer $\lnot P$.

So, it turns out that there are inferences we can make that aren't as simple as determining whether some rule's condition has been met or not!

How do we generalize this finding? Well, the first step is to make sure that our KB is in a particular format:

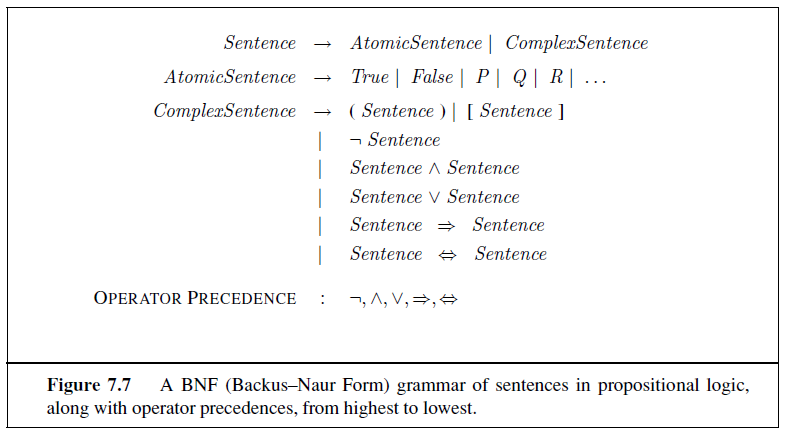
A logical sentence is in conjunctive normal form (CNF) if it consists solely of a conjunction of clauses with negations on propositions alone. Formally: $$Clause = P_1 \lor P_2 \lor ... \lor P_n \\ KB = Clause_1 \land Clause_2 \land ... \land Clause_k$$

Any logical sentence can be converted into CNF via two steps:

Rephrase all biconditionals and implications to use only $\lnot, \land, \lor$ connectives.
Push all negations "inward" so that negations are only applied to propositions.

In pursuit of converting into CNF, you may make use of the following propositional logic grammar and associated logical equivalence rules (from your textbook):

Let's look at an example from our Pitfall Maze Pathfinder from last time:

Convert the following sentence into CNF: $B_{1,0} \Leftrightarrow (P_{2,0} \lor P_{1,1})$.

The steps are as follows:

Step 1: convert all biconditionals and implications to use only the primitive connectives:

$$\begin{eqnarray} B_{1,0} \Leftrightarrow (P_{2,0} \lor P_{1,1}) &\equiv& (B_{1,0} \Rightarrow (P_{2,0} \lor P_{1,1})) \land ((P_{2,0} \lor P_{1,1}) \Rightarrow B_{1,0}) \\ &\equiv& (\lnot B_{1,0} \lor (P_{2,0} \lor P_{1,1})) \land (\lnot (P_{2,0} \lor P_{1,1}) \lor B_{1,0}) \end{eqnarray}$$

Step 2: push all negations "inward" so that they apply only to propositions (not groups of props like $\lnot (P \land Q)$):

$$\begin{eqnarray} (\lnot B_{1,0} \lor (P_{2,0} \lor P_{1,1})) \land (\lnot (P_{2,0} \lor P_{1,1}) \lor B_{1,0}) &\equiv& (\lnot B_{1,0} \lor P_{2,0} \lor P_{1,1}) \land ((\lnot P_{2,0} \land \lnot P_{1,1}) \lor B_{1,0}) \\ &\equiv& (\lnot B_{1,0} \lor P_{2,0} \lor P_{1,1}) \land ((\lnot P_{2,0} \lor B_{1,0}) \land (\lnot P_{1,1} \lor B_{1,0})) \\ &\equiv& (\lnot B_{1,0} \lor P_{2,0} \lor P_{1,1}) \land (\lnot P_{2,0} \lor B_{1,0}) \land (\lnot P_{1,1} \lor B_{1,0}) \end{eqnarray}$$

Observe that this last sentence is in CNF since it consists of 3 conjoined clauses:

$$\begin{eqnarray} (\lnot B_{1,0} \lor P_{2,0} \lor P_{1,1}) \land (\lnot P_{2,0} \lor B_{1,0}) \land (\lnot P_{1,1} \lor B_{1,0}) \equiv Clause_1 \land Clause_2 \land Clause_3 \end{eqnarray}$$

...where:

$$\begin{eqnarray} Clause_1 &=& \lnot B_{1,0} \lor P_{2,0} \lor P_{1,1} \\ Clause_2 &=& \lnot P_{2,0} \lor B_{1,0} \\ Clause_3 &=& \lnot P_{1,1} \lor B_{1,0} \end{eqnarray}$$

So why is a KB in CNF desirable? Well let's see...

Resolution

Let's revisit our earlier rain and sidewalk example, but with a KB that's in CNF:

KB:

"If it is raining, then the sidewalk will be wet" $\equiv$ "Either it's not raining or the sidewalk is wet"

1. $\lnot R \lor S$

"It is raining"

2. $R$

We know that we should be able to infer $S$ above, but what rule dictates this operation?

Note how (1) and (2) contain the same proposition $R$ but one has it in its negated form and the other in its positive--these can be combined, canceling out the contrasting prop and leaving only $S$ behind!

Resolution is a general form of Modus Ponens that operates on two clauses; if the clauses disagree on a propositions $P_i$ (i.e., one has $P_i$ and the other has its negation $\lnot P_i$), then a new clause can be inferred consisting of the union of propositions between the clauses except the disagreed-upon. Formally: $$\frac{(P_1 \lor P_2 \lor P_i \lor ...) \land (P_3 \lor P_4 \lor \lnot P_i \lor ...)}{P_1 \lor P_2 \lor P_3 \lor P_4 \lor ...}$$

Consider how each of the following clauses will be "resolved" (i.e., what can be inferred from them).

$Clause_1$	$Clause_2$	Resolution from $Clause_1 \land Clause_2$	Explanation
$\lnot R \lor S$	$R$	$S$	Since $\lnot R$ and $R$ disagree, we're able to infer the union of disjoined propositions from both clauses... it turns out that's just $S$.
$S \lor \lnot R \lor T$	$Q \lor R$	$S \lor T \lor Q$	Since $\lnot R$ and $R$ disagree, we're able to infer the union of disjoined propositions from both clauses, which is $S, T$ from Clause 1 and $Q$ from Clause 2.
$\lnot S$	$S$	$\emptyset$	Since $\lnot S$ and $S$ disagree, we're able to infer the union of disjoined propositions from both clauses, which is... well, nothing! This case represents when resolution can detect a logical contradition, since it is not possible to have a KB for which both $S$ and $\lnot S$ are mutually true.
$\lnot S \lor R$	$S \lor \lnot R$	$S \lor \lnot S \equiv R \lor \lnot R \equiv True$	This is the most often confused part of resolution: it is an operation defined on a single literal at a time! As such, we can choose to resolve on the $S$ literal OR the $R$ literal BUT NOT BOTH AT ONCE. The result is what is known as a vacuous sentence that is always logically equivalent to the constant $True$ (which is True in every world).

So how do we harness resolution in pursuit of a general KB query algorithm? Consider our previous approach and what we might do differently...

We have been practicing theorem proving (testing if a sentence is entailed by the KB) by seeing if the KB entails a query by the given rules of inference. Since this approach can meander (which KB components are relevant to our query or not?) what tool from your Methods of Proof class (probably your favorite approach) could we use instead?

Proof by contradiction!

Proof by Contradiction

Aha! Let's instead see if we can proceduralize the old proof by contradiction -- every proof student's attempt at simplifying a proof!

How does every proof by contradiction start? How can we analogize this start given our propositional logic KB in CNF form and some query sentence $\alpha$?

"Assume to the contrary..." as in, make an assertion that is knowingly false. In the context of our inference problem, this simply means adding the negation of our query to the KB! i.e., $KB = KB \land \lnot \alpha$.

How does "proof by contradiction" proceed? What is its goal and how can we translate it to our inference problem?

It attempts to show that by assuming the opposite of what was intended to be proved is true, we reach a contradiction. For our inference problem we can show that the addition of the negated query to the KB makes it inconsistent.

Formally, combining the above, we have a new approach to inference:

Given some CNF KB and query sentence $\alpha$, resolution proof by contradiction proceeds as follows:

Add the negation of the query to the KB: $KB = KB \land \lnot \alpha$
Apply pairwise resolution to all clauses, including those that are inferred by resolution until:
- $KB \land \lnot \alpha \equiv \emptyset$ meaning that resolution reached a contradiction. In this case, $KB \vDash \alpha$
- There are no other resolutions to consider, meaning that we've tried everything and not reached a contradiction. In this case, $KB \not \vDash \alpha$

Let's see how this works in our Pitfall Maze Pathfinding problem!

Consider a CNF KB with the following clauses and determine whether or not it entails the query $\lnot P_{1,0}$.

Disclaimer: for illustrative purposes, we'll omit some clauses that would normally be in the KB of this system.

KB: (using rule that $B_{0,0} \Leftrightarrow (P_{0,1} \lor P_{1,0})$ and fact $\lnot B_{0,0}$ in CNF)

$\lnot B_{0,0} \lor P_{1,0} \lor P_{0,1}$
$\lnot P_{1,0} \lor B_{0,0}$
$\lnot P_{0,1} \lor B_{0,0}$
$\lnot B_{0,0}$

Step 1: "assume to the contrary" that there is a pit in (1, 0), adds the following to the KB:

$P_{1,0}$

Step 2: iteratively apply resolution until we either reach a contradiction or run out of resolutions to try:

$B_{0,0}$ [Clauses 2 and 5]
$\emptyset$ [Clauses 4 and 6]

Aha! We derived the empty clause, therefore $KB \vDash \alpha$, i.e., $KB \vDash \lnot P_{1,0}$

Since we inferred that no Pit exists in (1,0), our agent is safe to move there!

Plainly, the above is just a simple example of proof by resolution, but we can at least get a gist for its mechanics and power in more complex scenarios.

We'll get some more practice with these later!

Practice

For variables P and Q, show, using both propositional (boolean) algebra and truth tables, that the following sentences are logically equivalent:

  P ⇒ ¬Q
  Q ⇒ ¬P

Use propositional algebra to convert the following sentence into CNF:

  ;; #1
  ¬(X ∨ Y) ∧ Z
  
  ;; #2
  (X ∧ Y) ⇒ Z
  
  ;; #3
  (X ∨ Y) ⇒ Z

Perform resolution and proof by refutation on the following KB to answer the question as to whether KB ⊨ α

  α = ¬X ∧ Y
  
  KB =
     1. X ∨ Z ∨ Y
     2. ¬Z ∨ W ∨ X
     3. ¬X ∨ W
     4. ¬W

\(Clause_1\)	\(Clause_2\)	Resolution from \(Clause_1 \land Clause_2\)	Explanation
\(\lnot R \lor S\)	\(R\)	\(S\)	Since \(\lnot R\) and \(R\) disagree, we're able to infer the union of disjoined propositions from both clauses... it turns out that's just \(S\).
\(S \lor \lnot R \lor T\)	\(Q \lor R\)	\(S \lor T \lor Q\)	Since \(\lnot R\) and \(R\) disagree, we're able to infer the union of disjoined propositions from both clauses, which is \(S, T\) from Clause 1 and \(Q\) from Clause 2.
\(\lnot S\)	\(S\)	\(\emptyset\)	Since \(\lnot S\) and \(S\) disagree, we're able to infer the union of disjoined propositions from both clauses, which is... well, nothing! This case represents when resolution can detect a logical contradition, since it is not possible to have a KB for which both \(S\) and \(\lnot S\) are mutually true.
\(\lnot S \lor R\)	\(S \lor \lnot R\)	\(S \lor \lnot S \equiv R \lor \lnot R \equiv True\)	This is the most often confused part of resolution: it is an operation defined on a single literal at a time! As such, we can choose to resolve on the \(S\) literal OR the \(R\) literal BUT NOT BOTH AT ONCE. The result is what is known as a vacuous sentence that is always logically equivalent to the constant \(True\) (which is True in every world).