Constraint Satisfaction Problems

Thus far, we've been approaching search problems wherein states are treated as atomic, indivisible, black-boxes that are either approved or rejected by some goalTest.

Maze Pathfinding: a state (maze cell) is either the destination / goal, or it isn't.
Changemaker: a set of coins either optimally sums to the target, or it doesn't.
LCS: a string is either the (one of) the longest common subsequences of two strings, or it isn't.

It turns out that these problems are just special cases of more general formulations in which we can decompose states in some meaningful ways.

Why do you think it would be useful to decompose a state into some constituent parts?

This allows us to identify which parts of a state are problematic (and therefore can be fixed in a more targeted fashion) and those parts that are correct.

That's a bit abstract, I know! Let's look at a classic example that describes these new types of search problems, and then reason as to how they're important to consider separately from search.

Map Coloring

In Map Coloring Problems, the goal is to assign one of $K \ge 2$ colors to entities on a geographical map (i.e., bodies like nations or nation-states) such that no two adjacent entities have the same color.

Consider the following map diagramming the Republic of Forns, a totally real nation state that you shouldn't bother Googling.

Now, before we find a solution to this very small Map Coloring problem, let's find a better representation for it.

What data structure might be useful for modeling the adjacencies between nation-states on the map such that we could then quickly check if its neighbors were the same color or not?

An undirected graph, where each node represents the nation-state, and an edge connects those that are adjacent.

We can then enumerate the constraints that any solution to this problem must adhere to.

Depicted, we have:

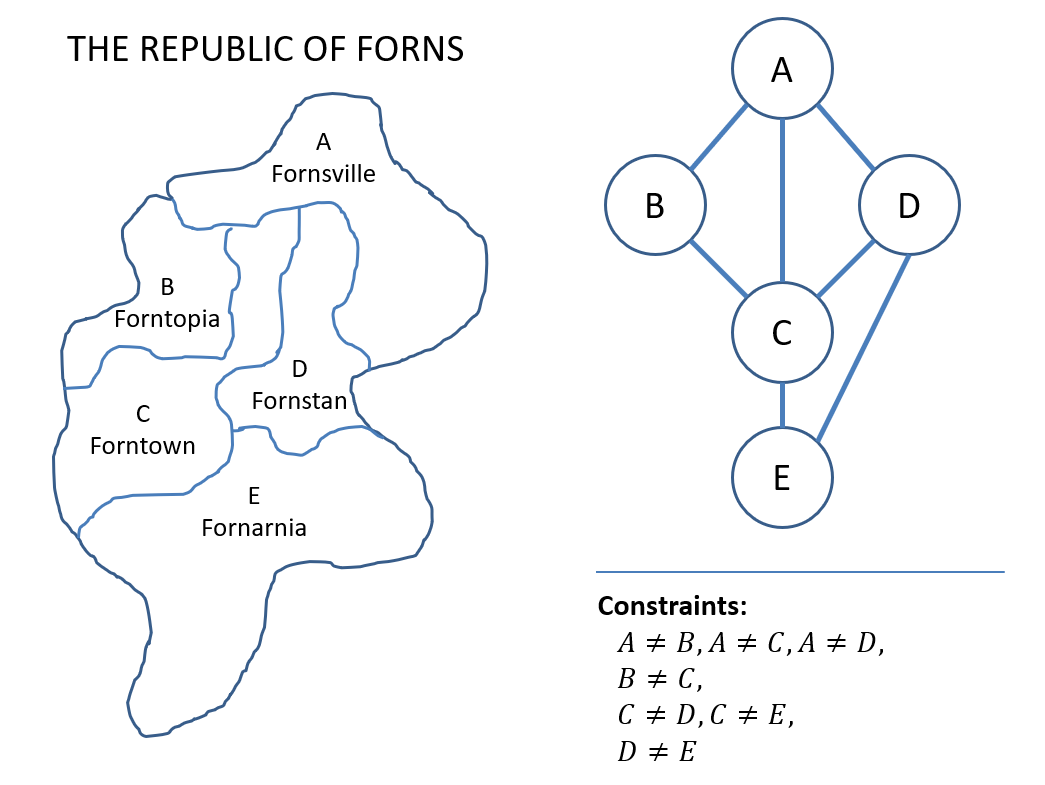
Graphs are easier to reason over, and we can easily check solutions using them.

Provide a solution to the Map Coloring problem of the Republic of Forns with $K = 3$ colors: Red, Green, Blue.

$$A = Red, B = Blue, C = Green, D = Blue, E = Red$$

Depicted:

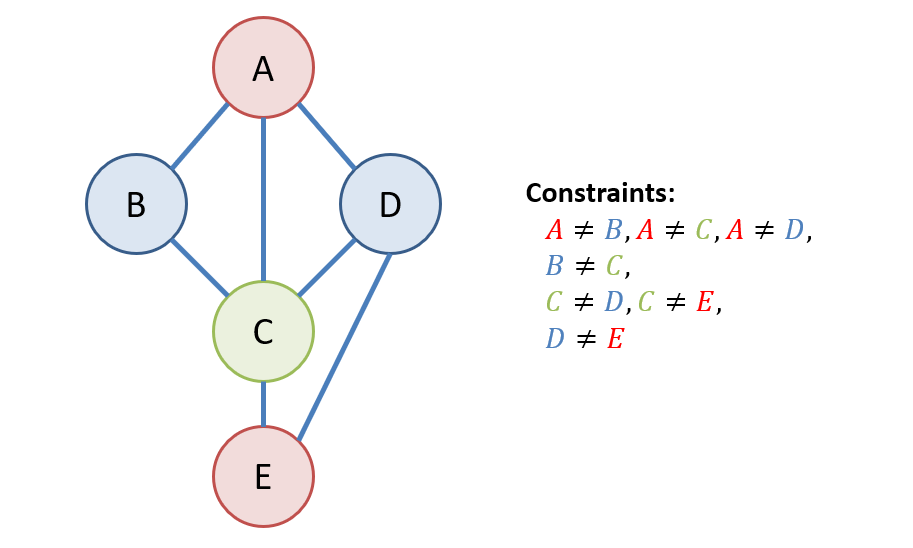
Reflecting on this small example:

[Reflection 1]: this may seem like a *trivially-solved problem,* but why might it (in general) be difficult?

Consider a map with 1000 nation-states -- if you assigned, e.g., Red to a nation-state early in some sequence of assignments, it may make the problem impossible to solve rather than had you assigned that same state Blue!

[Reflection 2]: this may seem like an *artificial* problem without real-world binding, but how do you think (as it pertains to map "coloring") it could be used in practice? [Hint: think of what each map area's color might signify].

Zoning: any SIM City fans out there? Puting an industrial complex next to a residential neighborhood is generally not considered good city planning. These tools can help section off districts to assign to certain purposes.

In brief, you can thank Map Coloring as the reason you probably didn't grow up next to a Nuclear Power Plant!

Of course, this is but one application of many served by formalizations of this particular algorithmic paradigm; let's do just that now to see how we might apply it to other domains as well.

Constraint Satisfaction Problems (CSPs)

Constraint Satisfaction Problems (CSPs) are those in which variables composing some problem state must be assigned some values that satisfy a set of constraints.

Just as we specified search problems as inputs into search algorithms, so too must we specify these CSPs.

A CSP is a 3-tuple $CSP = \langle X, D, C \rangle$ of components:

Variables $X$: a set of variables that stratify the state.
Domains $D_i$: for each variable $X_i \in X$, the domain specifies the legal values that $X_i$ can be assigned.
Constraints $C$: a set of boolean constraints that can be evaluated for the assigned value of each variable.

A CSP solution is an assignment of values to variables from their domains such that all constraints are satisfied.

To map (pun intended) these ideas to our Republic of Forns Map Coloring example, we could have specified this CSP as:

Variables: $X = \{A, B, C, D, E\}$ one for each nation state.
Domains: $D_i = \{Red, Green, Blue\}~\forall~X_i \in X$, the allowable colors that could be assigned each variable.
Constraints: $C = \{A \ne B, A \ne C, A \ne D, B \ne C, ...\}$, one for each adjacent nation-state.
Solution: $A = Red, B = Blue, C = Green, D = Blue, E = Red$

Now, we can see that for nontrivially sized problems, we'll need some means of systematically exploring the space of possible assignments of values to variables, which will indeed be some form of search BUT...

...that doesn't mean we can't still contrast our objectives with the above to how we thought about Classical Search problems, and the tools we used to approach them.

Classical Search vs. Constraint Satisfaction
Property	Classical Search	Constraint Satisfaction
States	Atomic / Black-box	Decomposable into Variables + Domains
Goal Test	A state is or isn't a goal.	More informative: an assignment of values to variables either does or doesn't satisfy all constraints, but we also learn which are not satisfied.
Purpose	Planning: care about solution path from initial to goal state.	Identification: care only about solution, not path that derived it.

With these distinctions in mind, can you think of some applications for specifying Constraint Satisfaction Problems?

Most applications are in resource allocation, but to name a few classics:

City Planning / Zoning: per the map-coloring example above, how to partition geographical spaces by purpose in which adjacency is significant.
Course / Meeting Scheduling: finding times / rooms in which some number of individuals are available to meet in a given week.
Electrical Engineering: circuit board layouts can be configured through some number of constraints for adjacencies.
Game Playing: Sudoku is one giant CSP!

So, having now seen the formalizations, an example, and some applications, let's move to the next reasonable step: the algorithmic one!

The above describes the "what" -- let's look at the "how" (to solve CSPs).

Backtracking

Constraint Satisfaction Problems can be applied to many different scenarios with whatever variables, domains, and constraints can be imagined, so long as we are able to specify the components as given in the previous section.

Consider the following abstract CSP demonstrating some numerical problem that must be solved:

The following describes a 3-variable numerical CSP:

\begin{eqnarray} X &=& \{R, S, T\} \\ D_i &=& \{0, 1, 2\}~\forall~X_i \in X \\ C &=& \{ \\ &\quad& R \ne S, \\ &\quad& R = floor(T / 2), \\ &\quad& S \lt T \\ \} \end{eqnarray}

Unlike the map-coloring problem from earlier, these are a bit more brain-teasing -- it's much harder to just squint at the above formalization and then arrive at a solution.

As such, we should have some means of approaching a solution systematically.

Let's start, per usual, with the "dumb" way of doing things, and see how we can do better.

Brute-Force

For the purpose of representing a fully-specified state, we will use a tuple notation such that an assignment of values to variables will look like: $$(R, S, T) = (0, 2, 1) \Rightarrow \{R = 0, S = 2, T = 1\}$$

If we were to brute-force a solution algorithm to this problem, what would that strategy look like?

Try all possible combinations, subjecting each to the goal test, and then continuing if it fails, i.e., trying: $$(0, 0, 0), (0, 0, 1), (0, 0, 2), ...$$

Why is this approach wasteful / dumb?

We end up trying quite a few combinations that we know *never* have a chance of working. E.g., any state with the format $(0, 0, T), (1, 1, T), (2, 2, T)~ \forall~t \in D_t$ will fail because they violate the first constraint.

What would be the computational complexity of this approach in terms of $n = |X|$ and $d = |D|$ (assuming all variables have the same domain)?

Exponential, yikes: $O(d^n)$ (for reasons that will be made clear momentarily)

This poor performance arises largely as a consequence of treating the state as an atomic entity that cannot be decomposed further!

[Brainstorm] How can we improve upon this approach?

Backtracking

We can still draw from our knowledge of solutions to Classical Search problems and adapt them to these now decomposable CSPs:

The standard Search Formalization of CSPs proceduralizes exploration of the variable assignment space as a search problem in which:

Search states in the search are defined as Partial Variable Assignments to those assigned values *thus far*
- The Initial State is thus the "empty assignment" (no values assigned to any variable).
- The Goal Test is thus a boolean response to a "complete assignment" (values to assigned to ALL variables) ensuring that the assignment satisfies all constraints.
Actions / Transitions are assignments to a *single* variable at a time (which then produces a state with that variable assigned).
Costs are assumed constant in most CSPs (though some variants will use "preferences" in place of costs).

Backtracking is an algorithmic paradigm in which depth-first search is performed on the recursion tree generated by the above search specifications with two additional requirements:

Fixed Variable Ordering: each ply of the resulting search tree assigns a value to a specific variable, and this ordering of variables is fixed from the start.
Incremental Goal Testing: subtrees are pruned as soon as a partial-assignment violates a constraint.

Some notes on the above:

The order of variables that we choose to assign to actually matters, but we'll look at that point later...
Pruning subtrees *as soon as* we make an assignment that creates an inconsistency is the hallmark of backtracking, since at that point (by the mechanics of DFS) we have "backed up" to another partial solution that "undoes" that problematic assignment.

Draw the CSP Search Tree that results from Backtracking search on our numerical example above in variable ordering: $R, S, T$

Notes on the above:

Note that depicted above is a *recursion* tree, not necessarily a search tree in which we are storing nodes; the backtracking is handled naturally by virtue of a return from a recursive call.
Note that this is a recursion tree, not a recursion graph; by virtue of assigning to only one variable at a time, and in a prescribed ordering, we will never see a repeated state.

Of course, none of the above is particularly new: we've equipped search with some new tools to suit a slightly different kind of problem, but we should take a second look at the above example...

In particular, we might be able to make some improvements on our backtracking technique through a couple of observations:

How might variable ordering be important? Suppose we decided to assign in order to $T, S, R$, how might this change things?
Are some domain elements doomed from the start? E.g., what does constraint #3 tell us about the possible domain elements of $T$?
What would be the process of discovering that there is *no solution* to a CSP using the above? Can we deduce this more quickly?

All these questions, and more, will be answered next time!