Observations and Experiments

Let's recap some of the lessons from last time...

• Causal Bayesian Networks add an extra assumption beyond tier-1 Bayesian Networks: that edges carry cause-effect relationships: $$X \rightarrow Y \Leftrightarrow f_Y(X)$$

• The notion of an intervention, encoded using the causal do-operator \(do(X=x)\) means we *force* \(X\) to attain the value \(x\) as by an external force or question of "What if?"

• Using an intervention is like making an inference in the *modified* model \(G_x\) where all inbound edges to \(X\) are severed.

• Performing inferences at tier-2 require that we provide a mapping between the network's parameters that we have (the CPTs) and the imagined parameters of the model in \(G_x\).

Whew! That's a lot! Sometimes, however, this is not a difficult task:

What was the difference between Markovian and Semi-Markovian Models?

Markovian = no unobserved confounders. Semi-Markovian = at least one unobserved confounder.

Why are Markovian models ideal for causal inference?

The probability distributions (CPTs) over variables in the unintervened graph \(G\) were the same as in the interventional setting \(G_x\) for intervention \(do(X = x)\).

This was nice because it allows us to ask and answer any causal query in terms of the network's original CPT parameters...

However, as we might imagine, this task becomes more complicated with Semi-Markovian domains, and to illustrate how it does, we turn to the problem of confounding as it's haunted the empirical sciences since the dawn of time.

Types of Data and Modeling

---

The type of data we have can not only inform the structure of a causal model, but can sometimes (alone) be used to answer queries of interest.

That perspective now relies on examining the different types of data that can be collected through different procedures and requires that we examine:

• How that data is situated in the causal hierarchy

• What those different types of data tell us about the "true" causal story / graph relating the variables in our models

We'll start with the weaker of those techniques...

Observational Data

---

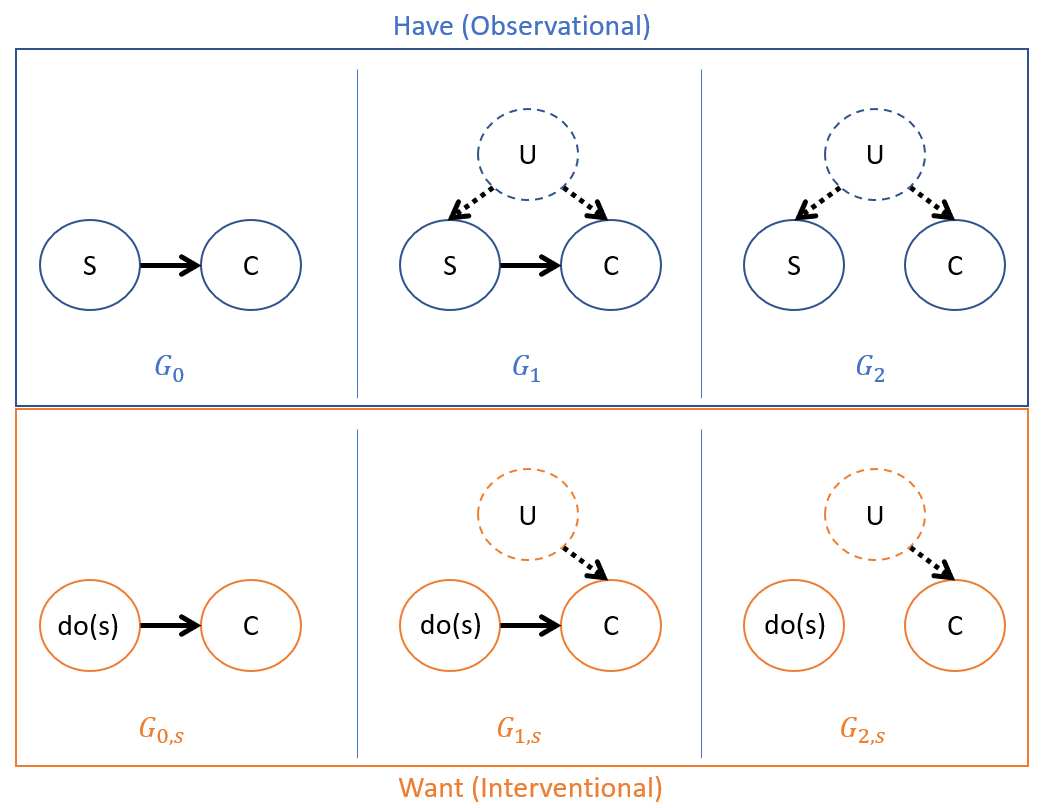
Suppose we wish to find the causal effect of Pre-cancer Smoking [S] on Lung Cancer [C] by estimating \(P(C|do(S))\) and have examined health records indicating a positive correlation, the problem being observational equivalence of desired CBN structures between the following:

(Assume that we have reasonable precedent to omit the \(C \rightarrow S\) cases because we're interested in *pre*-cancer smoking)

Notes on these models:

• All 3 that we *have* are observationally equivalent (same independence claims between the variables), and even if there is a causal effect between S and C, we can't rule out the presence of an UC.

• This means that the CPT parameters in each will be the same, but only in *some* will the probabilities in the unintervened setting (that we have) be the same as those in the interventional (that we want): $$P_G(V) \ne P_{G_{s}}(V)~\forall~V$$

Recall that this second bullet is problematic given the fact that causal queries must eliminate spurious correlations in order to be answered, and since the "true" model might not be the nice, Markovian \(G_0\), we may not be able to guarantee this.

Fun fact: If you think the \(G_2\) model is absurd, just note that it was the defense brought before the court in a landmark case against Philip Morris (the big cig manufacturer) in which \(U\) represented a genetic disposition to both smoke and attain cancer.

In order to both (1) disambiguate between the models above, and (2) answer the causal claim of interest, what procedure does the scientific community use in order to combat UCs and estimate causal quantities?

Randomized experiments, which disrupt the influence of any UCs on the treatment!

Funner fact: The one who made that Genetic Disposition argument above? Ronald Fisher, one of the fathers of experimental design!

Experimental / Interventional Data

---

Experimental data is acquired from randomized clinical trials, wherein some manipulation \(X\) is assigned to participants at random, creating an intervention (Tier 2): \(do(X = x)\).

In the event that some latent genetic disposition to smoking has influenced someone to smoke, that influence is disrupted if we intervened and *forced* different experimental groups to smoke, depicted below:

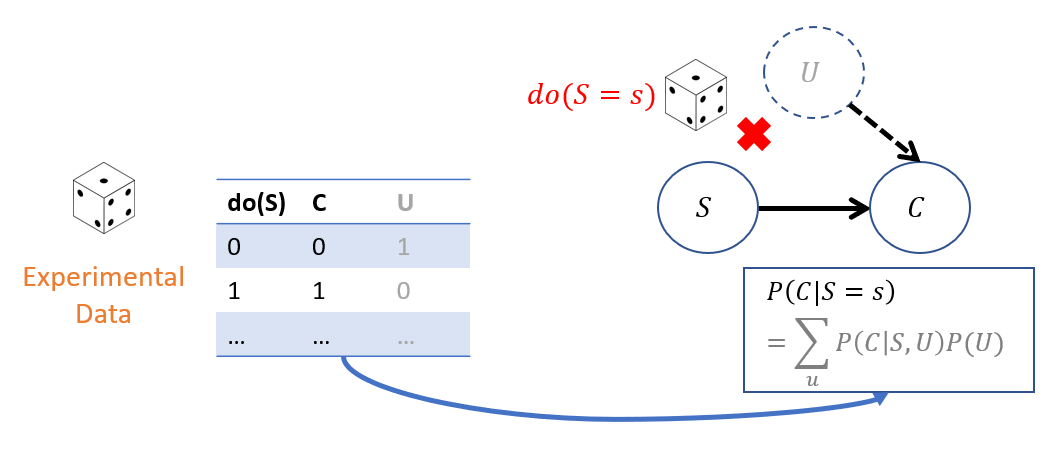
As such, any differences between groups that we forced to smoke and those that we forced to abstain from smoking, would be due to smoking alone (since the likelihoods of \(U=u\) in each group would be equivalent due to random assignment).

That said, what are some impediments to acquiring interventional data through a randomized experiment?

Experiments can be expensive, impractical, or (as demonstrated above) unethical!

Yeah did any of you blink an eye when I suggested we force people to smoke? Shame on you.

The takeaway: sometimes we have causal questions, but have only observational data. So, we need to know what questions can be answered with what we have, and which cannot!

Utility of Heterogeneous Data

---

Suppose we weren't particularly concerned with ethics and performed the Smoking experiment suggested above -- what question *haven't* we answered even though we might (through the experimental data) be able to estimate \(P(C|do(S))\)?

Which is the "correct" / "true" model in the unintervened setting!

Figuring out the true model despite knowing the answer to our query can be important for a couple of main reasons:

• It could be important that we know whether or not there are unobserved confounders in the "natural" setting that demand further inquiry.

• The relationship between \(S, C\) may be only a local portion of a larger causal model in which we care about a wider class of inferences that demand we know about the status of confounding.

Data collected on the same system, but through two different methods (e.g., observationally and experimentally) is sometimes considered heterogeneous data because the datasets contain different, inexchangeable information about the same variables.

Ethics aside, if we then performed an experiment wherein we randomly assigned participants to "smoke" and "don't smoke" conditions, we could determine the relationship between \(S, C\) with greater certainty.

Examining our "Want / Interventional" models in the example above, what would be the "true" model if the observational data says that \(C, S\) are dependent BUT the experimental data says that they are independent? I.e.,: \begin{eqnarray} G:~S &\not \indep& C \\ G_{s}:~S &\indep& C \end{eqnarray}

The true model here must be \(G_2\) because in the post-intervention world, \(G_{2,s}\) is the only one in which \(S \indep C\).

Nice! But this is the easy case, and not the one that really reflects reality... the harder question is as follows:

Examining our "Want / Interventional" models in the example above, what would be the "true" model if the observational data says that \(C, S\) are dependent AND the experimental data says that they are dependent? I.e.,: \begin{eqnarray} G:~S &\not \indep& C \\ G_{s}:~S &\not \indep& C \end{eqnarray}

From the independence relationships alone, it could be *either* \(G_0, G_1\), since the UC in \(G_1\) would also get interrupted by the randomized assignment.

Is there some way we could determine which is the right answer by looking at something in our 2 datasets that *isn't* just independence relations?

Yes! See if the answer to the risk difference and the ACE are different! If they are, then a confounder must be present to account for the difference.

This is a neat trick that has a formal definition:

The statistical test for confounding says that for two variables \(X, Y\) for which \(X \rightarrow Y\), confounding exists between them whenever: $$P(Y|X) \ne P(Y|do(X))~\exists y, x \in Y, X$$

Note that the above is sufficient evidence for confounding when the observational and experimental quantities differ, but when \(P(Y|X) = P(Y|do(X))\), it is only *highly unlikely* that confounding exists between \(X, Y\), but not impossible via a rare phenomenon known as invisible confounding (Forney & Bareinboim, 2019).

So, tl;dr:

• Defending one's causal model is no easy chore, and often relies on having access to some powerful assumptions, different forms of data, or the results of multiple experiments.

• However, CI provides the tools to both falsify and defend one's choice in model, as well as determining what kinds of queries it can and cannot answer.