It's time think beyond... the "What if?" and continue into the "What if something happened differently than it did?"

Note that these are subtly different questions:

• "What if?" is a question at tier-2 that imagines the impact of some hypothetical.

• "What if something happened *differently* than it did?" layers that hypothetical on *top* of some observed event that happened in reality, and may even *contrast* with it!

Consider our classic VHD and the counterfactual, "What's the likelihood we *would have* gotten heart disease, *had we not* vaped?" (implying that we did in fact vape and get heart disease). Visualize the flow of information from each part of this utterance.

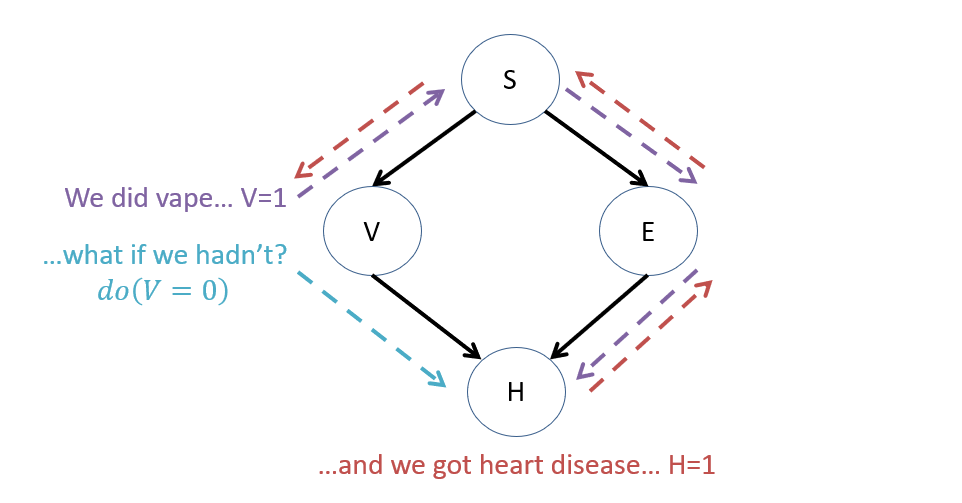
Some notes on this flow of information:

• The evidence of what happened in reality *tells us something* about the state of the system under which it happened.

• This *updated reality* (in which we did indeed vape and get heart disease) is somehow different than the "average" reality without that information.

• This means that our "What if" question might have a different answer than at tier-2 without that information, but is hard to annotate using our available do-operator, e.g., \(P(H|do(V=0),V=1, H=1)\) is syntactically invalid / nonsense because we can't have contrasting evidence and intervention at tier-2, nor a query for which there is observed evidence!

Counterfactuals as Causal Quantities

---

Let's see how our weird dude from Week 1 is doing climbing that causal hierarchy!

...well that was rude... you don't just call Einstein a nerd... Note wrong tho.

Intuitively, why do you think that the counterfactual layer is built atop the interventional (which, in turn, is built atop the observational)?

Because in practice, we cannot rewind time and see what would have happened if we chose differently; however, with the environment modeled as a system of causes and effects, we can sometimes *infer* what would have happened *differently* given any evidence of what *did.*

For this reason, we can think about counterfactuals as being a marriage of the previous two levels of the causal hierarchy: taking observations of what happened in reality and then hypothesizing a contrary intervention.

The good news: having a structural causal model (SCM) can help us predict what would have happened differently!

The intuition behind that:

• Knowing the causal functions of each variable can be important in predicting what would have happened differently than what did.

• Information about what happened in reality tells us something about the state of exogenous variables that account for some situational differences.

Let's start with a fan-favorite example to motivate the discussion of counterfactuals, which you might have seen already!

We'll reason first about the intuitions that we as humans would draw (automagically) in this setting, and then see how to proceduralize that process for our AI comrades.

Motivating Example: The Infamous Firing Squad

---

Things were getting a little to happy and philosophical in this class; let's ground ourselves in cold, hard reality with everyone's favorite example: the Firing Squad!

Rarely, prisoners whose crimes have been deemed egregious enough by the court marshal are put in front of the firing squad. The mechanics of this are unsurprising: A Court Verdict of Guilt \(G=\{innocent,guilty\}=\{0,1\}\) is issued for the firing squad, after which a captain of the guard \(C=\{abstains,signals\}=\{0,1\}\) gives the signal for 2 soldiers \(S_1,S_2=\{abstain,fire\}=\{0,1\}\) to fire. Both are good shots, so if either fire, the prisoner will die \(D=\{alive,dead\}=\{0,1\}\). The SCM modeling this scenario is defined as follows:

\begin{eqnarray} M:\\ U &=& \{G\} \\ V &=& \{C, S_1, S_2, D\} \\ P(u) &=& \{P(G=1) = 0.1\} \\ F &=& \{ \\ &\quad& C \leftarrow f_c(G) = G \\ &\quad& S_1 \leftarrow f_{s_1}(C) = C \\ &\quad& S_2 \leftarrow f_{s_2}(C) = C \\ &\quad& D \leftarrow f_{d}(S_1, S_2) = S_1 \lor S_2 \\ \} \end{eqnarray}

The graphical model for this is, of course:

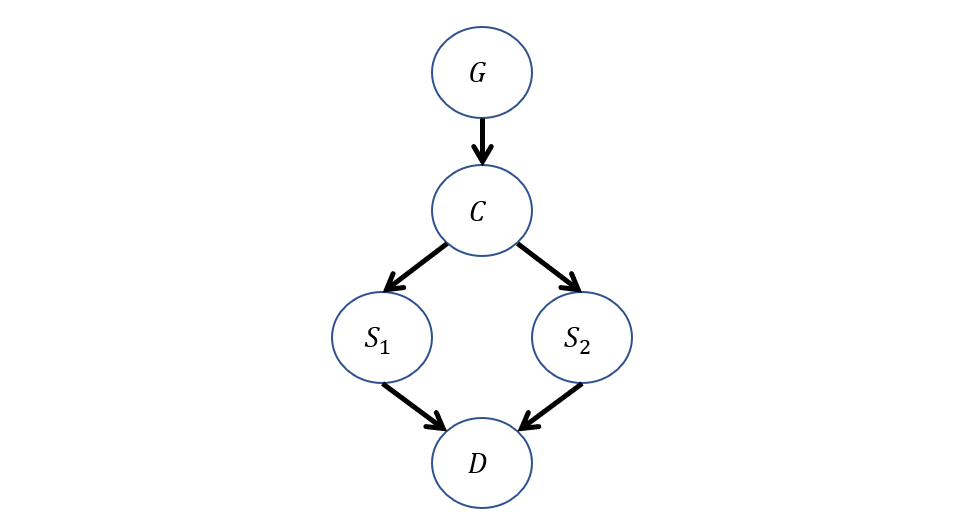
Now, let's ask some new queries and develop some intuitions about how to go about answering them!

Suppose we are interested in answering the question: "Would the prisoner have died had Soldier 1 not shot?"

This seems like a very human-expressable counterfactual query, but underneath it is some subtle evidence.

What evidence observed in reality is being subtly implied by this query?

That the prisoner died, and that Soldier 1 shot.

As a human interpreting the story / SCM above, how would you (intuitively) deduce the answer to this question?

Knowing that Soldier 1 *did* shoot means that the captain gave the order, which means that Soldier 2 also shot, meaning that even if Soldier 1 didn't, the prisoner still would have died.

Whew! That's some fancy logic right there, Sherlock! Yet, how intuitive it was for us as humans, because we have a tendancy to reason through these systems of causes and effects.

Wouldn't it be neat to automate this deductive process, and use it beyond simple models like the above?

You betchya! But let's think about the tools we've already developed thus far, and reason as to why they don't currently do this job:

How might we be tempted to formulate the query, "Would the prisoner have died had Soldier 1 not shot?" as a query from the causal / associational layers? Why would such a tool not make sense?

We might try to ask something like: \(P(D = 1|do(S_1 = 0), S_1 = 1, D = 0)\), but this is a gibberish expression! We're contrasting evidence and query, as well as the do-expression and accompanying evidence.

Yet, we still want to take information about the system from the observed evidence \(S_1 = 1, D = 0\) and then somehow, mentally, "rerun history" to see the effect of an intervention in that same setting.

This sounds tricky, but will follow according to the assumptions of our SCM!

So, we need to add to our causal vocabulary to answer counterfactual queries... let's develop some intuition for how to do this before we do.

Intuition: The Twin Network Model

---

So, to recap:

• Counterfactuals allow for observation and hypothesis to contradict.

• We cannot use the existing causal / associational notation to make sense of this.

• We are thus in need of some intuition for how to unite these observations and hypotheses.

Let's consider how to make this connection:

In a fully-specified SCM, what is the source of ambiguity / chance?

The exogenous variables, \(U\), since we assert that their state is decided by factors outside of the model. We encode this chance in the SCM via the \(P(U = u)\).

Intuition 1: In a fully-specified SCM, if we knew the state of all \(U\), we could determine the state of any \(V\).

This is, of course, true in only fully-specified SCMs; we can't always make such a claim in partially-specified SCMs like a Causal Bayesian Network.

Intuition 2: If we wanted to consider a counterfactual result, the state of \(U\) as it was observed in the real world should coincide with the state of \(U\) in the hypothetical world

This intuition corresponds with the idea that a counterfactual "reruns history" such that we wish to see a different action's effect in what is otherwise the same context / environment.

To unite these intuitions, we can think of counterfactuals as "bridging" the observed and hypothetical worlds in what has been called the Twin Networks Model.

The Twin Networks Model is a means of modeling the structure of a counterfactual query such that evidence observed in reality (the observational model, \(M\)) can be used to inform the hypothetical world, \(M_{X = x}\) (abbreviated \(M_x\)) for some counterfactual antecedent (what-if), \(X=x\). This is accomplished by sharing all exogenous variables \(U\) between \(M, M_{x}\), AND distinguishing variables in the interventional world with the subscript \(V_x\) notation.

Consider our previous query: "Would the prisoner have died had Soldier 1 not shot?" and observe how the Twin Network bridges the observed and hypothetical worlds.

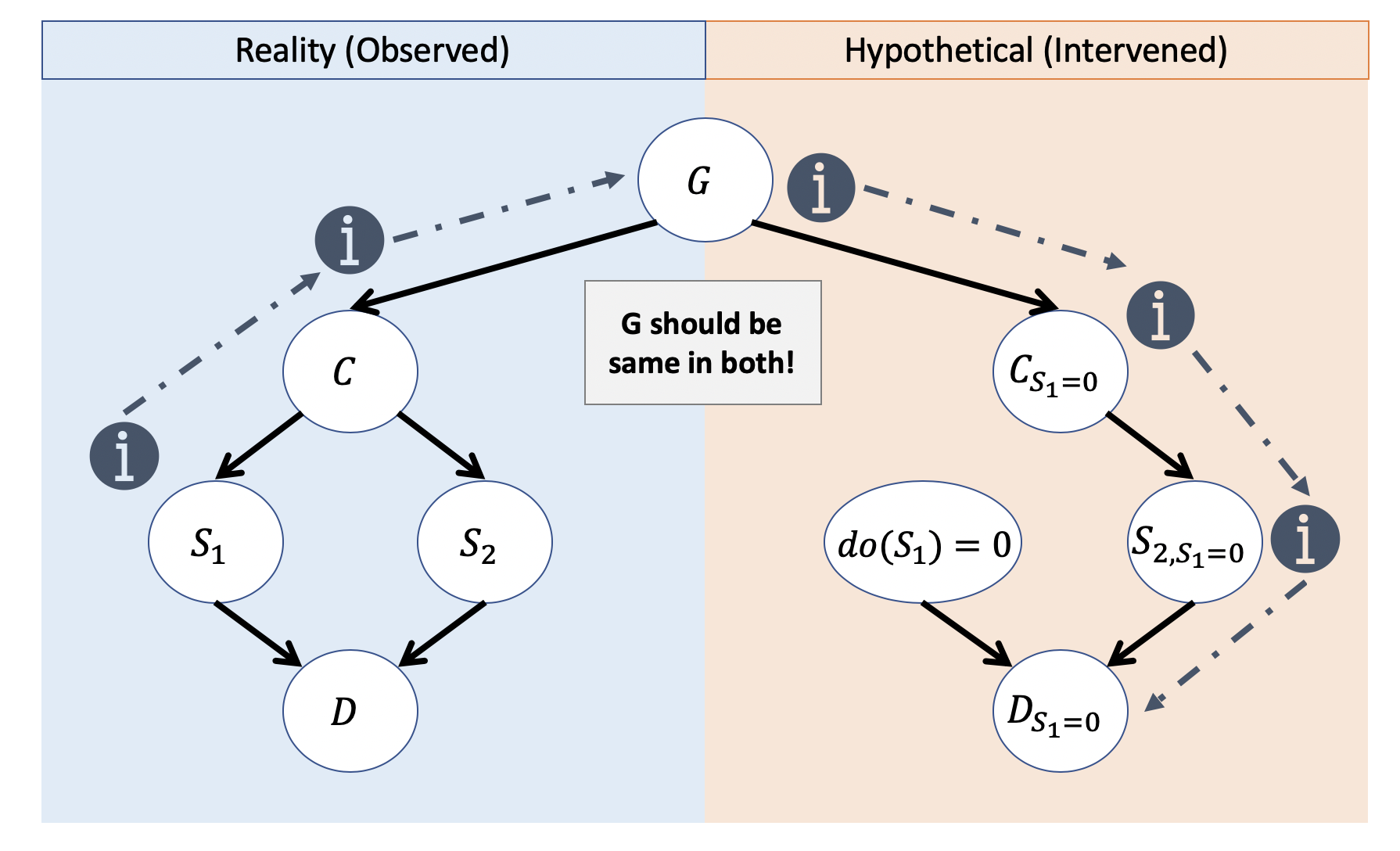
In words: Information that was observed updates our knowledge about the state of the exogenous variables, which we then use to compute the counterfactual in the hypothetical world wherein we make some interventional modification.

So, with this model in mind, let's look at some new notation and algorithms for computing counterfactuals! Yay!

Let's get the hard part out of the way first: the new notation.

Consider any two variables, \(X, Y\) in a SCM \(M\), let \(M_x\) be the modifed SCM wherein the structural equation for \(X\) is replaced by the constant \(f_x \leftarrow x\), and let \(U = u\) be an instantiation for the set of exogenous variables in the model. The formal definition of a counterfactual, "The value of Y had X been x" is: $$Y_{X = x} = Y_x = Y_{M_x}(u)$$ In words: \(Y_x =\) the solution to \(Y\) in the "surgically modified" model / graph \(M_x\) for a particular unit \(U = u\).

For brevity, we'll often just use one of the left-two notations like \(Y_{X=x}\) or \(Y_x\).

This definition is scarier looking than it actually is.

Twin Network Interpretation: Restated, the definition of a counterfactual \(Y_x\) simply says to compute the value of \(Y\) in the hypothetical component of the twin-network, given any evidence about \(U\) in the observational component.

This notation becomes a bit more intuitive when we see its relationship to some familiar ones... let's take a look!

Counterfactual Axioms

---

Since counterfactuals are the king-of-the-hill on the causal hierarchy, it makes sense that we can express the previous layers using the counterfactual notation as well.

So, let's look at some of the axiomatic characterizations of how we can express causal and associational quantities in counterfactual notation.

Interventional Equivalence: since \(Y_{X=x}\) represents "The value of Y had X been x", without any other evidence to update our belief about \(U\), we have the following equivalence: $$P(Y_{X=x}) = P(Y | do(X=x))$$

Consider again the twin network model; if there is *no* evidence being learned from the observational side, then what we're left with is just the interventional side, in which belief about \(Y\) will be the same as though we were just hypothesizing the causal effect of \(X\) on \(Y\) (i.e., \(P(Y|do(X))\)).

Neat! How about the observational layer?

Consistency Axiom: whenever the observed value of some variable \(X = x\) is the same as the hypothesized counterfactual antecedent \(Y_{X = x}\), then the observed and hypothetical worlds are the same world! This leads to the equivalence: $$P(Y_{X=x} | X = x) = P(Y | X = x)$$

So, this just leaves one case remaining: a "true" counterfactual, wherein observed and hypothesized values of some variables may disagree.

"True" Counterfactual: although a counterfactual, in the causal framework, is any useage of the variable-subscript notation like \(Y_x\), a "true" counterfactual quantity is one in which observed and hypothesized values of a variable disagree, allowing us to write: $$\exists x \ne x' \in X,~P(Y_{X=x} | X=x')$$

The above "true" counterfactual \(P(Y_{X=x} | X=x')\) represents the query, "What is the probability of \(Y\) had \(X = x\), given that it was, in reality, some different \(X = x'\)"

So, in this new counterfactual notation, how would we write our Firing-Squad query of, "Would the prisoner have died had Solider 1 not shot?"

$$P(D_{S_1 = 0} = 1 | S_1 = 1, D = 1)$$

With this notation in mind, let's consider how to compute an arbitrary query of this format!

Three Step Counterfactuals

---

In a fully-specified SCM, computing counterfactuals of the format \(P(Y_x | e)\) can be done in 3-steps.

Let's rejoin a simplified version of our orignal query in the firing-squad example. \(P(D_{S_1 = 0} = 1 | S_1 = 1)\).

Step 1 - Abduction: Takes observed evidence and updates belief about the exogenous variables, \(U\). In a fully-specified model, we solve for \(U = u | e\) (for evidence \(e\), or update \(P(u) \rightarrow P(u|e)\) for non-deterministic fully-specified SCMs).

Our running Firing-squad example is a fully-specified model, so we can solve for \(U = u | e\).

Consider again our twin model. For the query \(P(D_{S_1 = 0} = 1 | S_1 = 1)\), what exogenous variables must we solve for, and what is the evidence that we're updating them with?

Exogenous variable: \(G\); Evidence to update it with: \(S_1 = 1\).

Visually, that will look like the following:

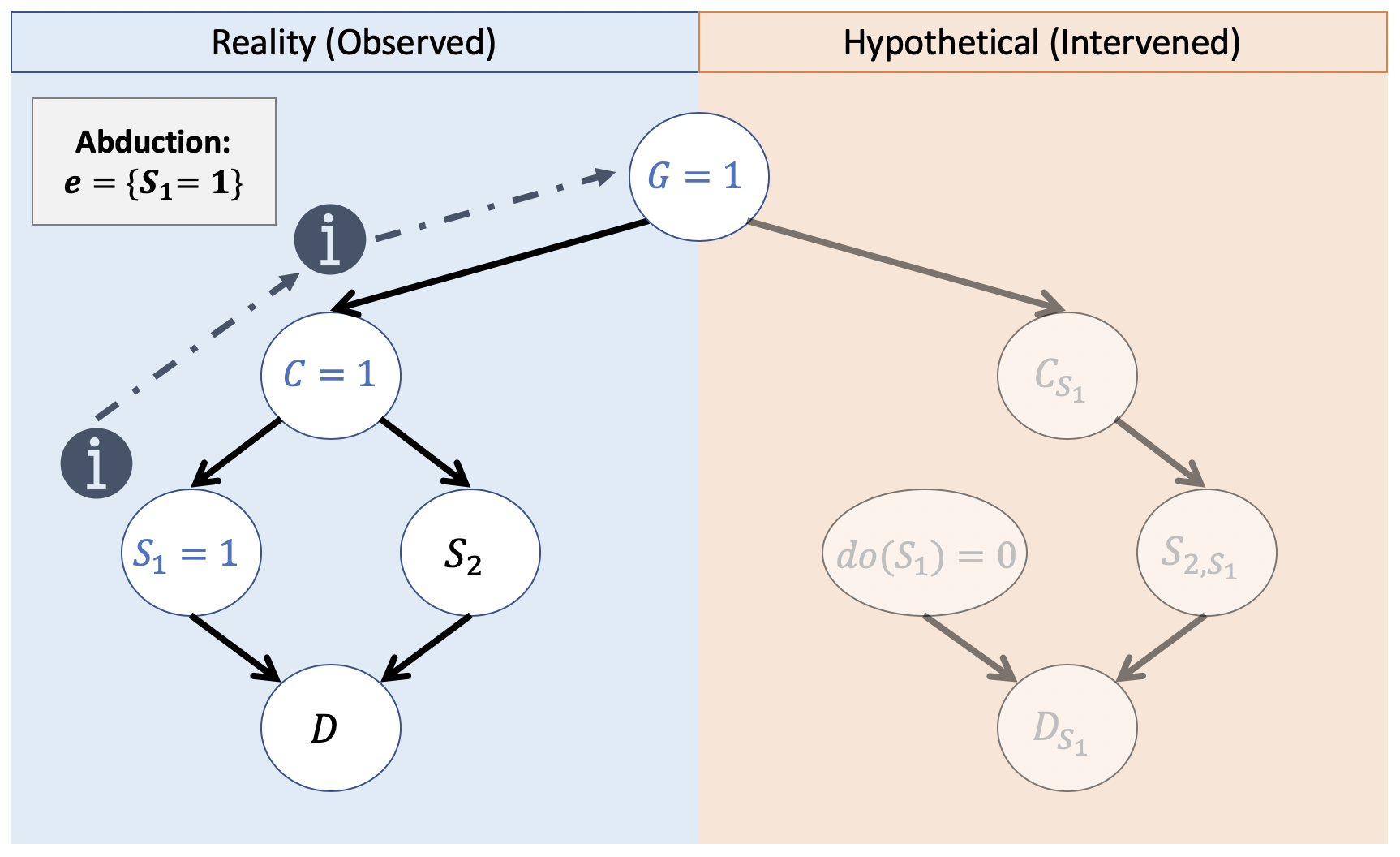
This is due to the fact that, with the structural equations:

\begin{eqnarray} S_1 &\leftarrow& f_{s_1}(C) = C = 1 \Rightarrow \\ C &\leftarrow& f_{c}(G) = G = 1 \Rightarrow \\ G &=& 1 \end{eqnarray}

So, we've successfully solved for all \(U\), in this case, we know that observationally, \(G = 1\) in order for us to have seen \(S_1 = 1\).

Step 2 - Action: Modify the model \(M\) by removing the structural equation for the counterfactual antecedent \(X\), and replace them with the fixed constant \(X = x\).

In the twin network conception, this simply means: shift your attention to the right side of the diagram now.

If we were doing this inference procedure in-place (on a single model), step 2 would transform the updated "real world" in the the "hypothetical world" in the twin network.

For us, though, we'll just now visualize the right side of the model with the updated values of the exogenous variables (in this case, just \(G = 1\)).

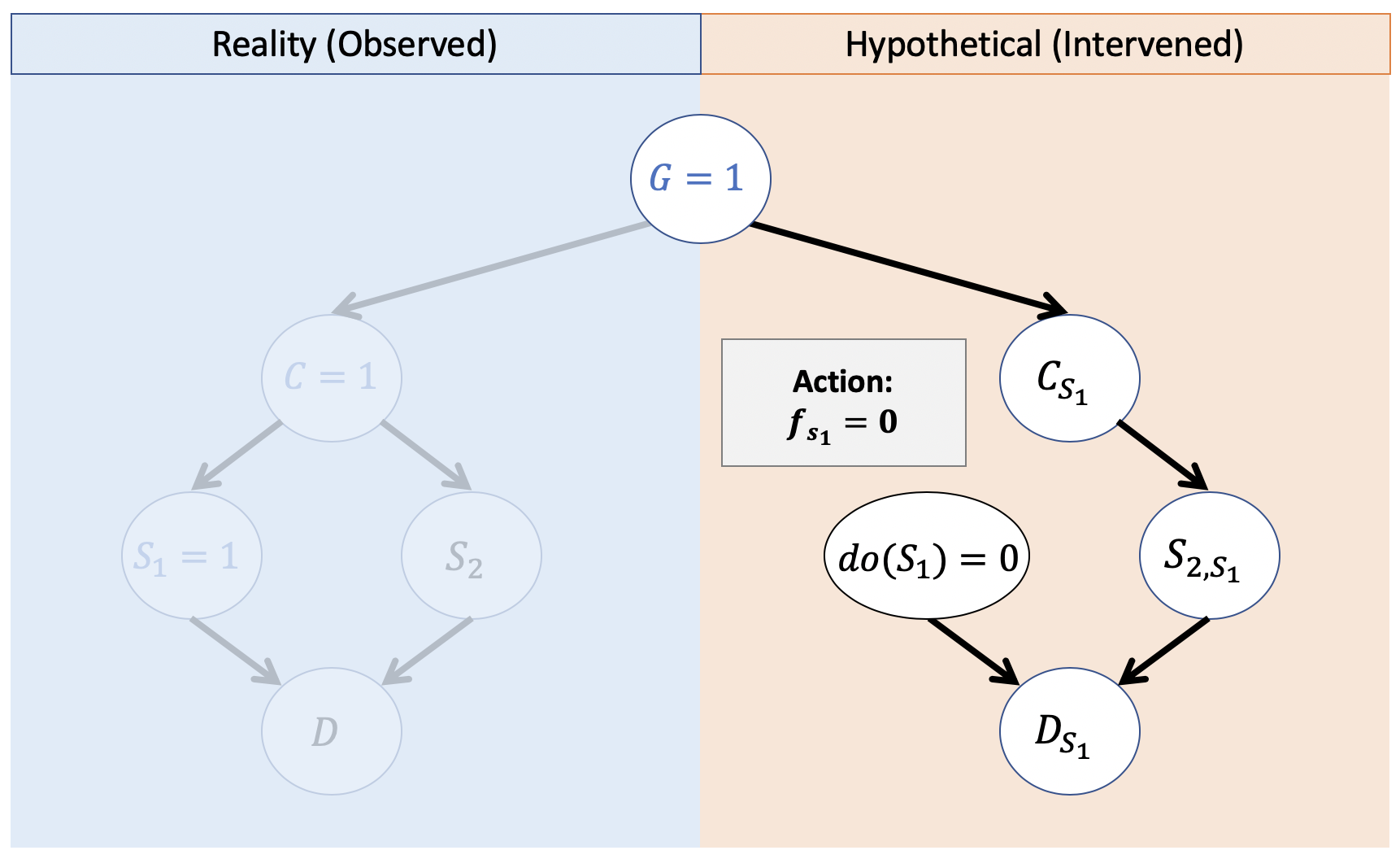
We are now poised for the coup de grace... the final answer awaits us in this hypothetical network!

Step 3 - Prediction: In the modified model \(M_x\), and with the updated \(U = u | e\) (or \(P(u|e)\) for non-deterministic fully-specified SCMs), solve for the query variable \(Y_x\).

In our fully-specified model, this just means we plug-and-chug! In a partially specified one, we would perform standard Bayesian inference here.

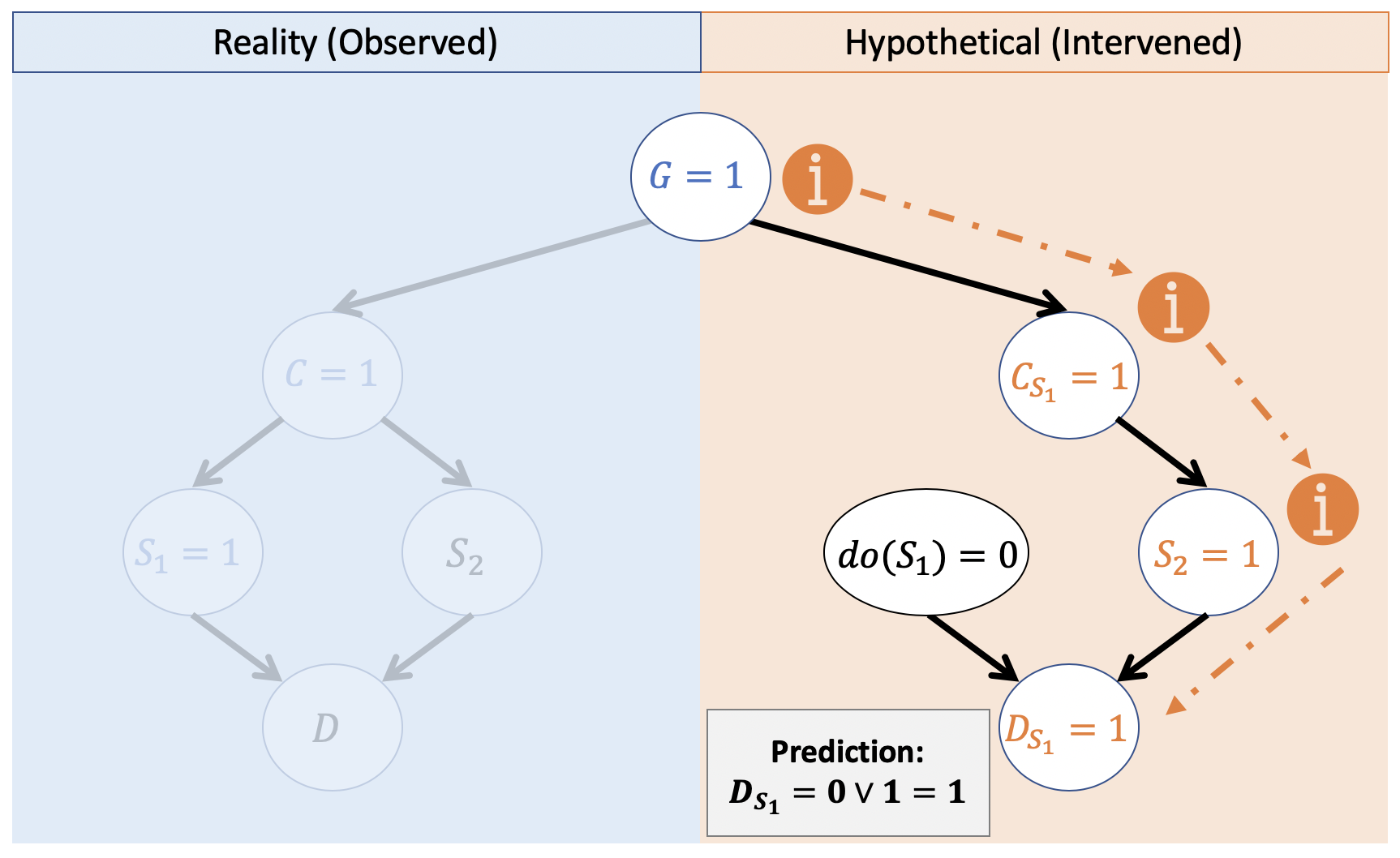
So, in this hypothetical part of the twin network, we simply solve for \(D\):

\begin{eqnarray} C &\leftarrow& f_{c}(G) = G = 1 \Rightarrow \\ S_2 &\leftarrow& f_{s_2}(C) = C = 1 \Rightarrow \\ D &\leftarrow& f_{d}(S_1, S_2) = S_1 \lor S_2 = 0 \lor 1 = 1 \end{eqnarray}

Tada! In probabilistic syntax, we would thus have: \(P(D_{S_1 = 0} = 1 | S_1 = 1) = 1\); it is certain that the prisoner would still die.

Note how this matched our human intuition for the answer to this query -- but now, we have a procedure for it!

Next time: more counterfactuals, wahoo!