We begin our journey into the fascinating world of causal inference by examining one of the most important fruits to come from the field: the causal hierarchy.

The Causal Hierarchy describes a 3-tiered perspective of the types of data, models, and queries that can be answered, with each tier (theoretically) subsuming the capabilities of the ones beneath it.

Powerfully, this hierarchy provides not only a way of thinking about the techniques that we deploy in AI, but also how we think about... thinking! There are many human-level cognitive capacities that are difficult to describe outside of its formalization.

Indeed, both cognitive systems designers (CMSI) and cognitive scientists (PSYC) care about studying the causal hierarchy, seeing how human cognition falls within its tiers, and thinking about how to automate its tools for the betterment of intelligent systems.

Causality for Cognitive Scientists

---

Observation 1: Humans still practice associational reasoning at times... for better and worse!

What are some examples of associational thinking that humans practice, and when ?

These are akin to the System 1 processing mentioned above: the fast, effortless, quick processing that we often rely upon to survive! Don't want to sit and pine on the magic of thermodynamics when our hand is burning on the stove, better let reflex move our hand before we think about it to avoid damage.

Yet, it's a good thing we don't *only* make reactionary decisions, and recruiting the cortex to really think things through is what gives us humans that iconic edge at the top of the intellectual food chain (though the aliens reading this may be giggling at that sentence).

If you haven't read it, pick up a cope of "Thinking Fast and Slow" by Kahneman and think about how System 1 and System 2 processing maps to the causal hierarchy.

Name some other examples of when humans practice detrimental associational reasoning.

Observation 2: Humans are naturals at assigning cause-effect relationships by way of explaining the world around us.

Provide an iteratively widening explanation for why someone might have a headache.

Why might such a model of explanations be useful to us?

For understanding our environment and importantly: for determining just what our actions should change to better it!

Observation 3: Blame and regret are counterfactual in nature and link reinforcement to attribution!

Add a tequila node to the headache explanation graph above for illustration of this!

Punchline: humans think in terms of cause and effect to our benefit of decision-making, question-asking, and learning in many powerful ways from which autonomous agents could likewise benefit.

Causality for Computer Scientists

---

Observation 1: Don't expect an associative intelligence to be able to answer causal queries successfully!

Take, for example, ChatGPT -- an absolute *marvel* of associative intelligence that plainly has many use cases... but is infamously poor at providing answers beyond the associational tier of what it's *seen*.

Observation 2: Purely associational agents can be biased and therefore, potentially unethical!

What do you notice about the following responses from ChatGPT?

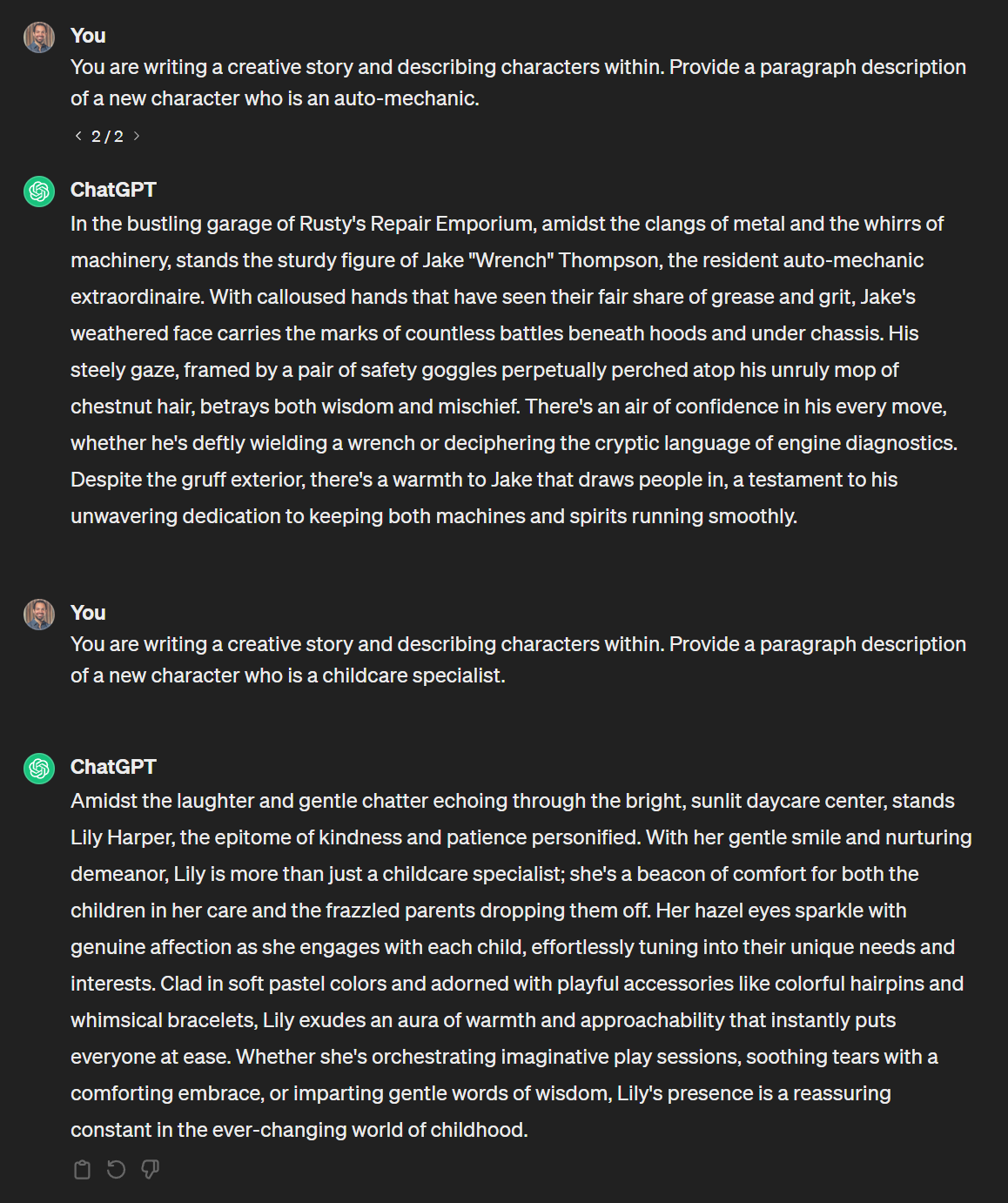
What could explain the bias exhibited above?

ChatGPT consumes of huge amounts of past data in which the proportion of descriptions of certain professions map to historical gender roles, so its own descriptions will likewise conform to that data.

Punchline: if our intelligent systems are inescapably bound to the data / experiences they've seen, they will not be able to evolve or think beyond it!

Important Comparisons

---

Mega-Punchline: now throw in signals of reward and punishment that BOTH humans and AIs "experience" (in our own ways). Causality now has a lot to say about many of the problems of RL from the first half of the course!

Provide some examples of Reinforcement Learning problems that might have some answers in the study of causality?

• Feature selection: how do we choose what the important features are for making decisions and maximizing reward?

• The attribution problem: how do we know what parts of our decision vs. environment were to blame for a received reward?

• Learning from regret: can we more carefully make changes to a policy based on experiences we regretted?

• Many more!

Let's think a bit about how we can frame our discussion about causality and motivate some tools needed to accomplish it.

Let's start by considering why causality is important for decisions in a variety of circumstances: both in population-level policy-making and individualized decision-making.

Let's start with a fundamental question that we'll end up formalizing later.

[Brainstorm] What is meant by a "cause + effect" relationship between two variables?

Most answers will dance around the idea of the "DNA of the universe" that we talked briefly about at the start of the class.

A convenient way of thinking about cause-and-effect is in a functional format:

$$\text{effect} \leftarrow f(\text{cause1}, \text{cause2}, ...)$$

Pearl's "Listening" Analogy: a variable \(Y\) that is affected by another \(X\) "listens to it" to obtain its value.

Most causal queries focus on designating systems of variables as (1) actions = treatments where an agent makes a choice, (2) outcomes describing variables we wish to affect with that choice, and (3) contexts = covariates that have some relationship to (1) and/or (2).

For each of the causal questions displayed, give an example for why answering them is of some value to us humans as decision-makers.

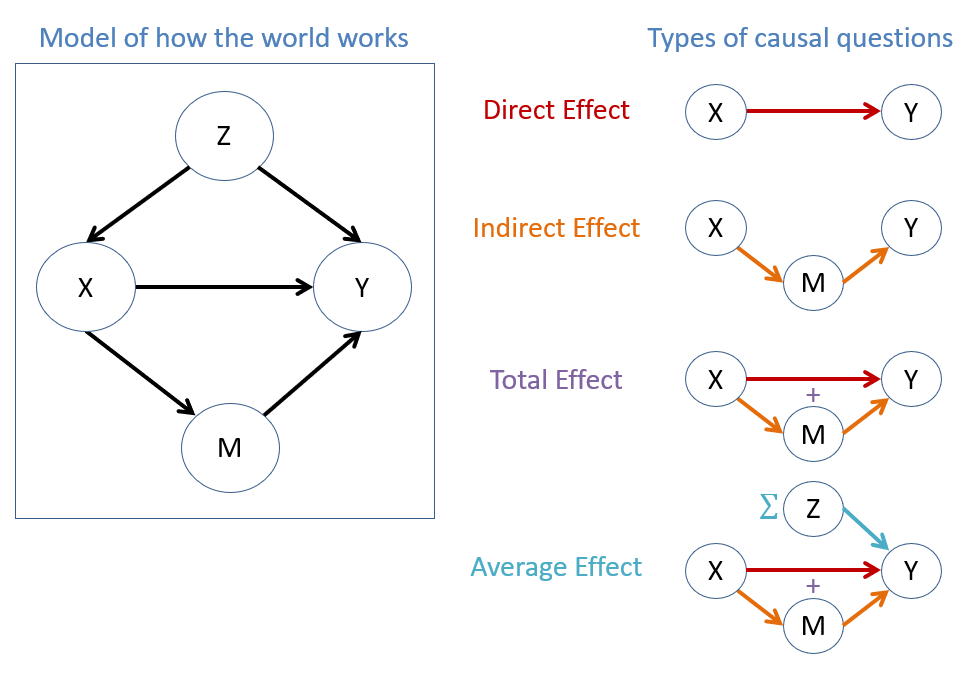
Hey, that model kinda looks like a structure we've spent a lot of time thinking about in the past... what is it?

A Bayesian Network!

In fact, most of modern causal inference found its... Bayes... in good old BNs, extending them to the more expressive models we'll learn about later.

Still, we'll lean on some of the same tools we talked about in the past to build up to those, so it's important to remind ourselves of tier 1:

Today, we begin our ascent of the Causal Hierarchy! We'll take some baby-steps with review to start, and then finish climbing in a little more than a month (wow, big ladder!)

In fact, we've already been introduced to the first wrung from AI, so let's take a moment to re-acquaint ourselves (since a break has separated us and that material, and therefore our memories have been basically wiped).

At the Associational / Observational tier of the Causal Hierarchy, we model, and can answer inference queries about, how variables in the system have been observed to covary.

This layer captures associations as they are observed in reality; NOT as they COULD be differently.

In the probabilistic semantics, this translates to what variables are independent of what other variables, and how information seen about one variable informs another.

Noteworthy: we know that any probabilistic expression can be evaluated from the full joint distribution (in tabular terms, the Joint Probability Table): $$P(A, B, C, ...)$$

That said, what was the problem with maintaining the full joint distribution of variables, and what solution did we explore?

As we model more variables in the system, the JPT grows exponentially! As such, we observed that the JPT can be factored using independence and conditional independence relationships between variables using a Bayesian Network.

That's right, our old friends Bayesian Networks are back, and since they're at the foundational layer of the Causal Hierarchy, we should take some time to remember them!

BNs consist of two primary components to parsimoniously encode the joint distribution. What were these components?

Let's look at the nitty-gritty now.

Bayesian Networks: Structure

---

We mentioned that the structure of the BN graph encodes the independence relationships between variables in the system.

What algorithm / ruleset allows us to answer whether any two variables \(X, Y\) are independent given another set, \(Z\), and summarize its rules.

Directional Separation (d-separation / d-sep for short).

The rules for d-sep are summarized below:

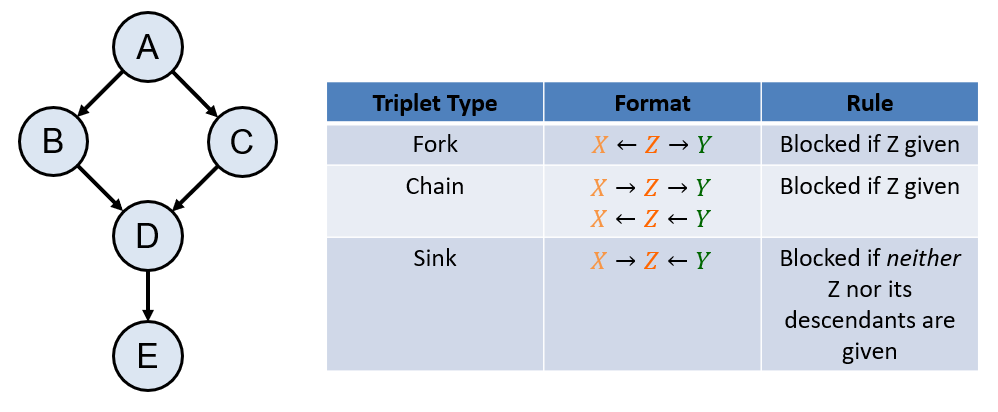
For review, verify that the following relationships hold in the example graph to the left using the rules of d-separation: $$A \indep D~|~B, C$$ $$B \indep C~|~A$$

Bayesian Networks: Semantics

---

To motivate the semantics of a Bayesian network, let's consider a semi-realistic decision-making problem that might be relevant to your New Year's Resolution(s):

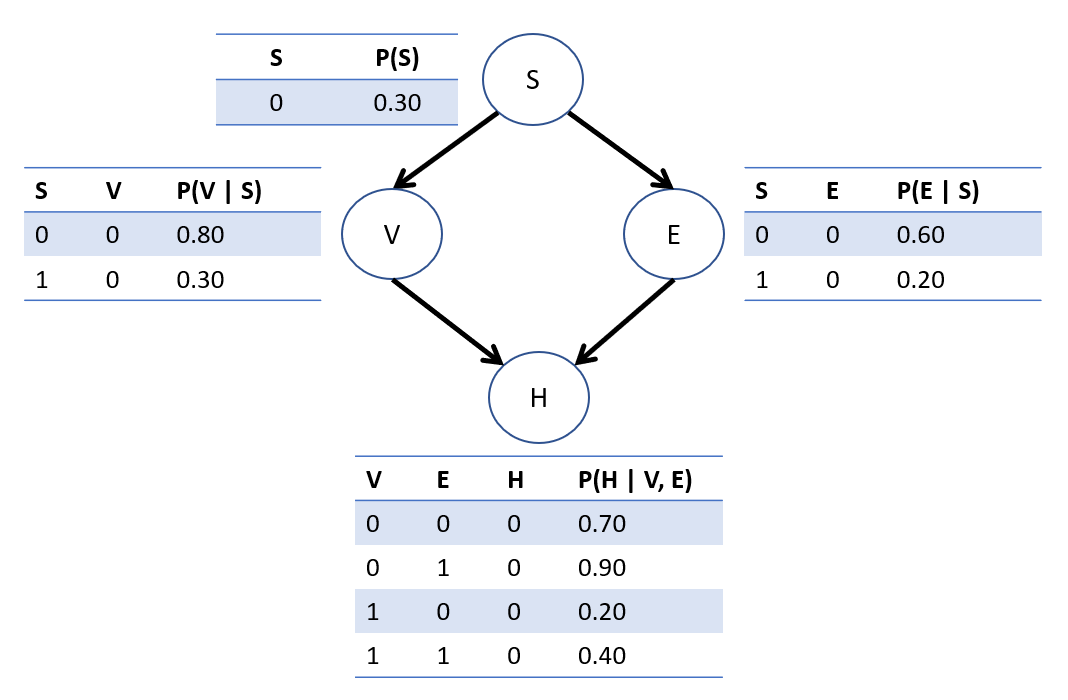
Suppose we wanted to know the probability that someone is stressed, vapes, doesn't exercise, and has heart disease; i.e., we want to compute: $$P(S = 1, V = 1, E = 0, H = 1)$$ How can we formalize, and easily answer, this using the network parameters (i.e., the CPTs)?

Bayesian Networks: Inference

---

Of course, for exact inference with arbitrary evidence, we need some more sophisticated methods than simply using the Markovian Factorization... but the MF will certainly help!

Let's try it!

Using the heart-disease BN above, compute the probability that an individual has heart disease, \(H = 1\), given that they vape, \(V = 1\).

Let us now take our first steps up the Causal Hierarchy and ask a very simple question to see whether or not we currently have the tools to answer it.

Suppose we have the heart-disease BN in the previous section and wish to know whether or not Vaping leads to (i.e., causes) higher risk of Heart Disease. In other words, we want to find the direct effect of \(V \rightarrow H\). What approach might you be tempted to take to answer this question?

Causal Queries Demand Causal Models

Notice that the query in question is a causal one: "Does vaping cause heart disease?"

Why is the difference between \(P(H = 1 | V = 1) - P(H = 1 | V = 0)\) NOT the answer to this query using a Bayesian Network?

Let's take a closer look at issue #1 now, and we'll tackle issue #2 in the next section.

BNs for Causal Inference - Problem 1: Observationally Equivalent models have the same set of independences but different causal implications.

Consider our heart disease network once more, and observe the following two observationally equivalent models. Consider the data that these models are meant to explain, and contrast the independence relationships between variables and the causal implications in each.

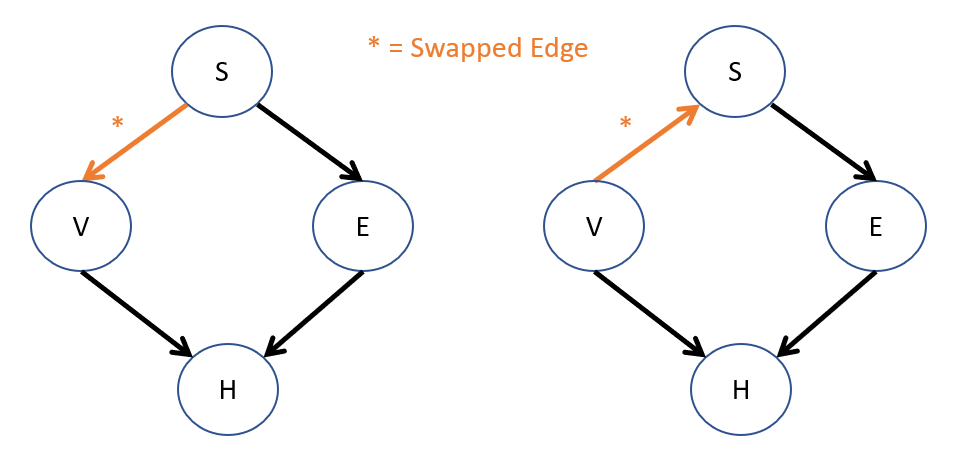
Rule of thumb: models that are observationally equivalent will almost always have the same sinks!

Note: Although BN structures are *motivated* by cause-effect relationships, an arrow from, e.g., \(S \rightarrow V\) simply means that they are directly dependent, but provides no guarantee that \(S\) *causes* \(V\).

Why is this a problem for decision-making in the VHD network with respect to the relationship between \(V, S\)?

If we interpret these BN structures as causal, then in the left model, people vape *because* they're stressed (which might relieve it), but in the right, vaping *causes* stress.

Note that the term "observationally" equivalent is meant to highlight that both of these models suffice to perform associational inference (for which any observational query will return the same answer in each), but that we would expect a directed edge \(A \rightarrow B\) to encode a cause-effect relationship if we want to answer causal questions.

This has thusfar been the chief purpose of BNs: to model these systems of probabilities and independences, but not necessarily to answer causal queries.

Using the Bayesian conditioning operator lands us in the second pool of hot water:

BNs for Causal Inference - Problem 2: Spurious Correlations can be introduced by the Bayesian conditioning operator (i.e., observing evidence) because of the way "information flows" through a BN in that non-causal information can flow between variables.

To visualize the problem:

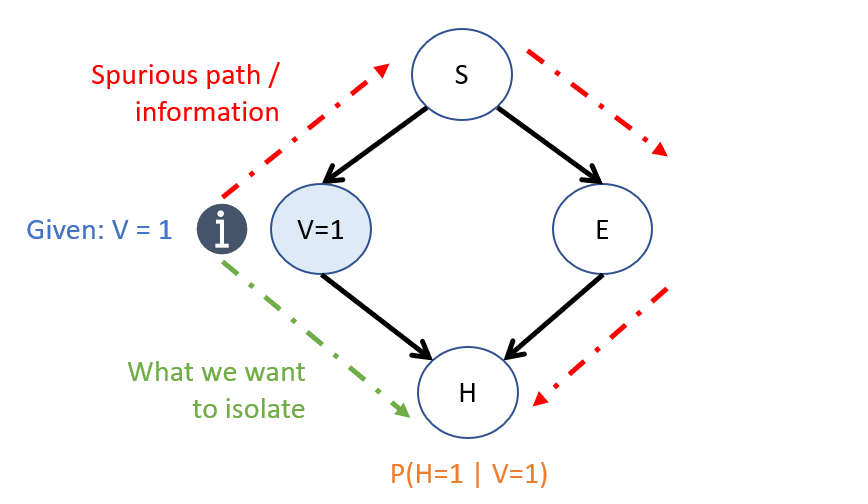
In words: SEEING information about \(V=1\) provides information about \(S\), which provides information about \(E\), which then provides information about \(H\) that is *tangential* to the causal query we want to answer. The only thing we want to know about is how \(V\) affects \(H\) directly.

One of the major tasks of Causal Inference is thus to isolate what part of the relationship between variables is causal and what part is merely associational. This is no easy challenge!

BNs for Causal Inference - Problem 3: Latent Common Causes may explain the dependence between variables, which are variables that are not recorded / observed in the system, but affect two or more of those that are.

In our example, this would be akin to not having recorded a participant's stress levels, or some other variable, that would explain the dependence between their propensity to vape and exercise.

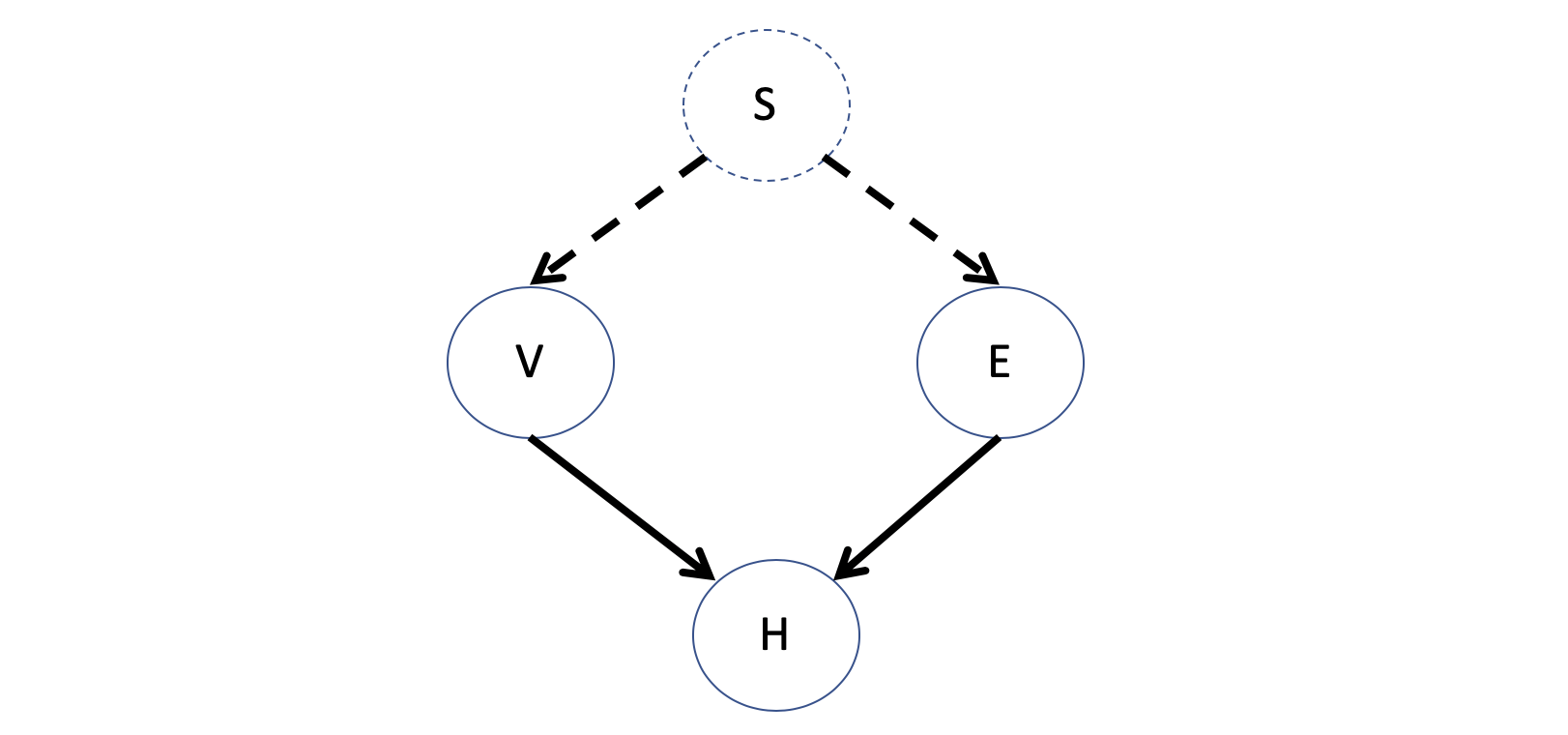
These present serious issues to causal inference because if, suppose, we were to model the dependence between V and E with a directed edge, the causal implications of the BN change (viz., that vaping will have some effect on exercise, which we know is actually not the case in the "true" model).

In general, it will not be possible to involve all relevant variables into our model, so instead, we will need a language that is able to clearly confess what pieces it has entirely and what pieces it does not.

With these predicaments in mind, we return to our CI Philosophy of Science suggesting that there is a "DNA of the Universe" that decides how the universe works.

If we want to add some causal assertions to our model to "capture" this DNA of the Universe, we'll need a (slightly) new language to do so...